|
Уравнения касательной и нормали
|
||||||||||||
|
Уравнение касательной в декартовых координатах
Предположим, что функция y = f(x) определена на интервале (a, b) и непрерывна в точке x0 ∈ (a, b). В этой точке (точка M на рисунке 1) функция имеет значение y0 = f(x0).Пусть независимая переменная в точке x0 получает приращение Δx. Соответствующее приращение функции Δy выражается формулой
Δy = f(x0 + Δx) − f(x0).
На рисунке 1 точка M1 имеет координаты (x0 + Δx, y0 + Δy). Построим секущую MM1. Ее уравнение имеет вид
y − y0 = k(x − x0),
где k − угловой коэффициент, зависящий от приращения Δx и равный
  Возможны два вида касательных − наклонные и вертикальные. Определение 1. Если существует конечный предел  , то прямая, имеющая уравнение , то прямая, имеющая уравнение
y − y0 = k0(x − x0),
называется наклонной касательной к графику функции y = f(x) в точке (x0, y0).Определение 2. Если предельное значение k при Δx → 0 является бесконечным:  , то прямая, имеющая уравнение , то прямая, имеющая уравнение
x = x0,
называется вертикальной касательной к графику функции y = f(x) в точке (x0, y0).Важно отметить, что 
y − y0 = f '(x0)(x − x0) или y = f '(x0)(x − x0) + f(x0).
Поскольку угловой коэффициент прямой равен тангенсу угла наклона α, который прямая образует с положительным направлением оси абсцисс, то справедливо следующее тройное равенство:
k = tan α = f '(x0).
Уравнение нормали в декартовых координатах
Прямая, перпендикулярная касательной и проходящая через точку касания (x0, y0), называется нормалью к графику функции y = f(x) в этой точке (рисунок 2).Из геометрии известно, что произведение угловых коэффициентов перпендикулярных прямых равно −1. Поэтому, зная уравнение касательной в точке (x0, y0):
y − y0 = f '(x0)(x − x0).
можно сразу записать уравнение нормали в виде

Уравнения касательной и нормали в параметрической форме
Пусть плоская кривая задана параметрически:
x = x(t), y = y(t).
Тогда угловой коэффициент касательной, проведенной в точке (x0, y0), находится по правилу дифференцирования параметрически заданной кривой:
  
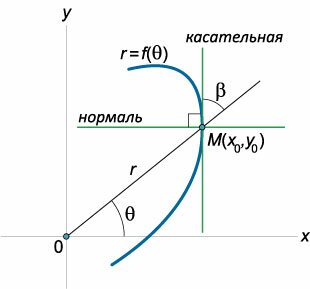
Уравнения касательной и нормали в полярных координатах
Предположим, что кривая задана полярным уравнением r = f(θ), выражающим зависимость длины радиуса-вектора r от полярного угла θ. В декартовых координатах такая кривая будет описываться системой уравнений
   Тангенс угла β вычисляется по формуле  
|
||||||||||||
|
Пример 1
|
||||||||||||
|
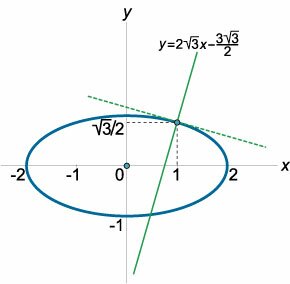
Написать уравнение нормали к эллипсу
 Решение.    |
||||||||||||
|
Пример 2
|
||||||||||||
|
Под какими углами кривая y = x3 − x пересекает ось абсцисс?
Решение.    |
||||||||||||
|
Пример 3
|
||||||||||||
|
Написать уравнения касательной и нормали к графику функции y = x√x − 1 в точке x = 2.
Решение.  
y(2) = 2 ⋅ 1 = 2.
Находим уравнение касательной:
  |
||||||||||||
|
Пример 4
|
||||||||||||
|
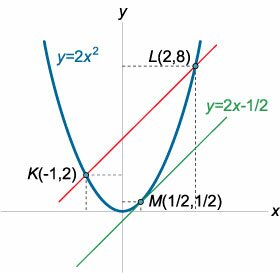
Дана парабола y = 2x2. Через точки параболы с координатами x = −1 и x = 2 проведена секущая (рисунок 5). Найти касательную к параболе, параллельную данной секущей.
Решение.   Найдем координаты точки касания из условия y'(x) = k:   
|
||||||||||||
|
Пример 5
|
||||||||||||
|
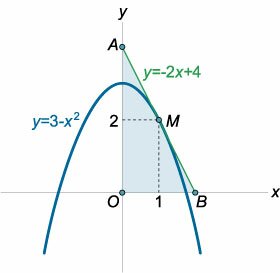
Определить площадь треугольника, образованного касательной к графику функции y = 3 − x2, проведенной в точке (1, 2), и осями координат (рисунок 6).
Решение.     |
||||||||||||
|
Пример 6
|
||||||||||||
|
Парабола задана уравнением y = x2 + 2x + 3. Составить уравнения касательных к параболе, проходящих через точку A(−1, 1).
Решение.  Найдем уравнения двух касательных к параболе, проходящих через точку A(−1, 1). Каждая из этих касательных определяется уравнением  Таким образом, задача сводится к определению угловых коэффициентов касательных k1 и k2. Учтем, что в точках касания B и C выполняется условие  
k = 2x + 2.
В результате мы имеем систему двух уравнений
 
1) касательная AB: x1 = −2, k1 = −2;
2) касательная AC: x2 = 0, k2 = 2.
Тогда уравнения касательных к данной параболе записываются в виде
1) касательная AB: y = −2x − 1;
2) касательная AC: y = 2x + 3.
|
||||||||||||
|
Пример 7
|
||||||||||||
|
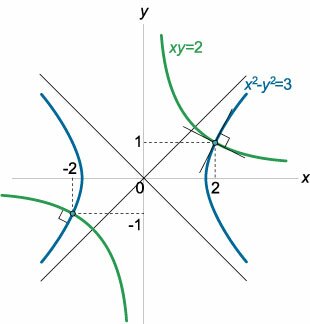
Доказать, что кривые x2 − y2 = 3 и xy = 2 пересекаются под прямым углом.
Решение.        |
||||||||||||
|
Пример 8
|
||||||||||||
|
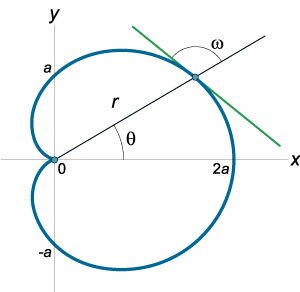
Найти угол между касательной к кардиоиде r = a(1 + cos θ) и радиусом-вектором точки касания.
Решение.    
|
||||||||||||
|
Пример 9
|
||||||||||||
|
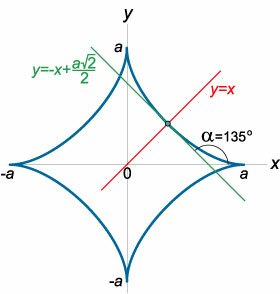
Найти уравнение касательной и нормали к астроиде x = a cos3t, y = a sin3t в точке t = π/4 (рисунок 10).
Решение.  
− tan t = tan(π − t).
Так как tan α = y'x = tan(π − t), то угол α составляет
     |
||||||||||||
|
Пример 10
|
||||||||||||
|
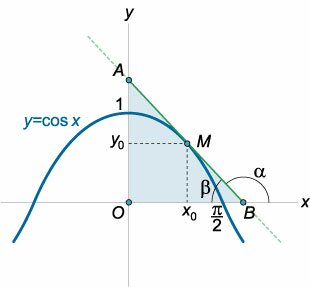
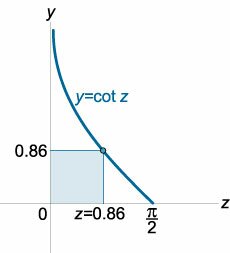
К графику функции y = cos x проведена касательная в точке M(x0, y0), где 0 < x0 < π/2 (рисунок 11). Найти значение x0, при котором площадь треугольника, образованного касательной и осями координат, будет наименьшей.
Решение.
y'(x) = (cos x)' = − sin x,
то угловой коэффициент касательной составляет
tan α = − sin x0 = y'(x0).
Тогда уравнение касательной имеет вид
          Приближенную координату точки минимума можно вычислить, например, в Excel. Она составляет примерно 0.86 рад или 49,3°.
|
||||||||||||