|
Производная функции в полярных координатах
|
||||||
|
Положение точек на плоскости можно описывать в различных системах координат. Помимо прямоугольной декартовой системы координат широко распространена также полярная система координат. В ней положение любой точки M описывается двумя числами (рис.1):
Например, Архимедова спираль (рис.2) описывается полярным уравнением 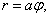 Переход от полярных координат  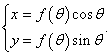 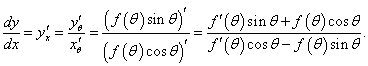 |
||||||
|
Пример 1
|
||||||
|
Найти производную dy/dx Архимедовой спирали.
Решение. 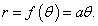 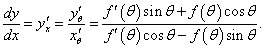 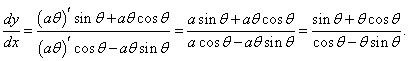 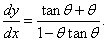 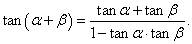  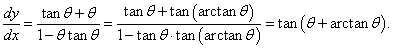 |
||||||
|
Пример 2
|
||||||
|
Найти производную dy/dx кардиоиды, заданной уравнением
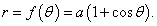
Решение.
Предварительно вычислим производную полярной функции:
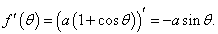 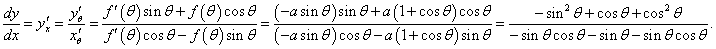 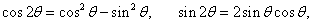 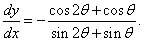 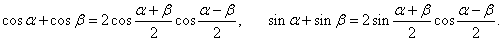 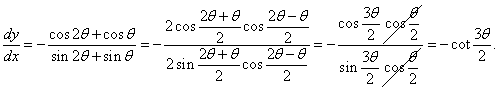 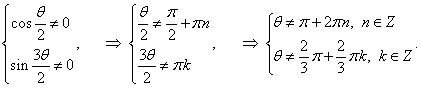 Кривая кардиоиды (рис.3) напоминает изображение сердца (отсюда происходит ее название) и обладает рядом замечательных свойств.
|
||||||
|
Пример 3
|
||||||
|
Найти производную dy/dx логарифмической спирали, заданной уравнением
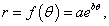 Решение. 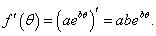 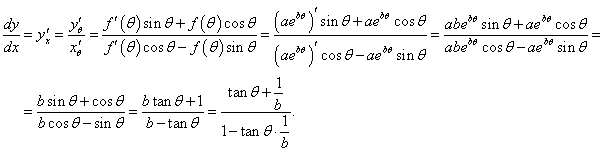 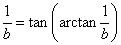  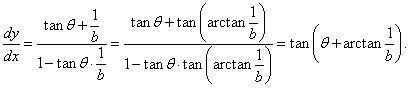
|
||||||
|
Пример 4
|
||||||
|
Найти производную dy/dx окружности и вычислить ее значения для полярных углов
Решение. 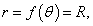 Отсюда, учитывая, что 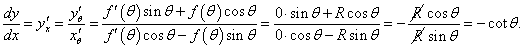 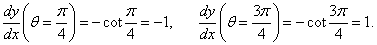
|
||||||
|
Пример 5
|
||||||
|
Найти производную dy/dx лемнискаты Бернулли, заданной уравнением
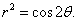
Решение.
Будем рассматривать данную кривую в интервале углов, при котором
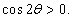 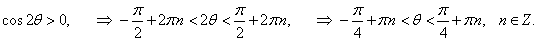 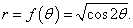 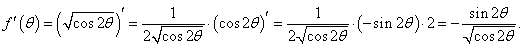 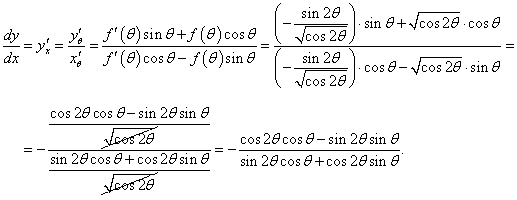  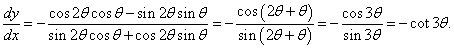 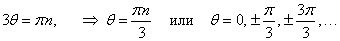 |
||||||
|
Пример 6
|
||||||
|
Найти производную dy/dx спирали Галилея.
Решение. Пусть тело начинает падать из некоторой точки A, расположенной над экватором Земли (рис.9). Движение вдоль радиус-вектора r является равноускоренным и определяется соотношением 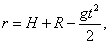
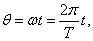 Таким образом, параметрические уравнения кривой имеют вид: 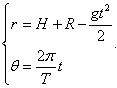 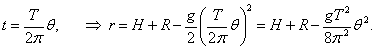 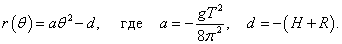 Акцентируя внимание на переменном (квадратичном) члене aθ2, рассмотрим далее случай 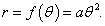 Определим производную найденной полярной функции: 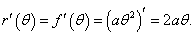 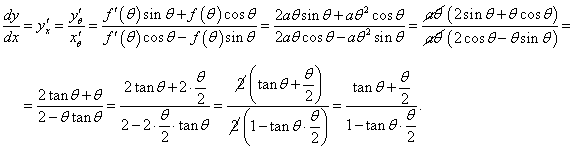 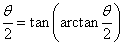 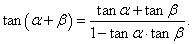 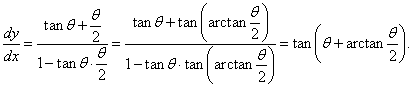 |
||||||
|
Пример 7
|
||||||
|
Найти производную dy/dx спирали Ферма, заданной полярным уравнением
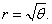
Решение.
В спирали Ферма радиус r с увеличением угла θ возрастает по корневому закону, т.е. достаточно медленно. Плотность витков увеличивается с ростом r, как видно на рисунке 11. Такой тип спиралей также встречается в природе. Например, семена в подсолнечнике размещаются вдоль кривых, напоминающих спираль Ферма (рис.12).
Находим сначала производную 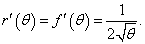 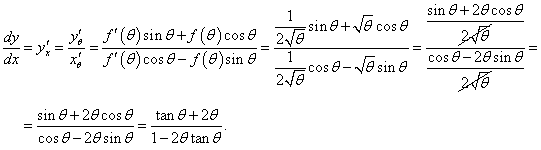 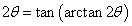 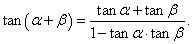 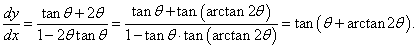 |
||||||











