|
Производная функции, заданной параметрически
|
|
Зависимость между аргументом x и функцией y может быть задана в параметрическом виде с помощью двух уравнений
 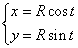 Найдем выражение для производной параметрически заданной функции. Предположим, что функции x = x(t) и y = y(t) дифференцируемы в интервале α < t < β, причем x' (t) ≠ 0. Кроме того, будем считать, что функция x = x(t) имеет обратную функцию t = φ(x). По теореме о производной обратной функции можно записать 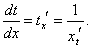 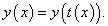 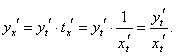 В приведенных ниже примерах найти производную параметрически заданной функции. |
|
Пример 1
|
|
x = t 2, y = t 3.
Решение.
Находим производные x и y по параметру t:
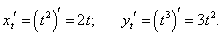 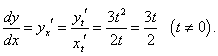 |
|
Пример 2
|
|
x = 2t + 1, y = 4t − 3.
Решение.
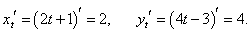 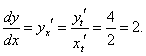 |
|
Пример 3
|
|
x = e 2t, y = e 3t.
Решение.
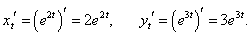 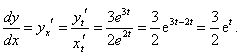 |
|
Пример 4
|
|
x = at, y = bt2.
Решение.
В этом примере производные по t равны
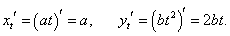 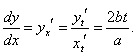 |
|
Пример 5
|
|
x = sin2 t, y = cos2 t.
Решение.
Дифференцируем по параметру t:
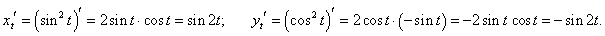 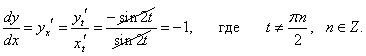 |
|
Пример 6
|
|
x = sh t, y = ch t.
Решение.
Вычислим производные:
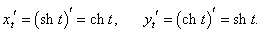 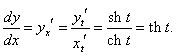 |
|
Пример 7
|
|
x = acos t, y = bsin t.
Решение.
Данные уравнения описывают эллипс с центром в начале координат и полуосями a и b. Продифференцируем переменные x и y по параметру t:
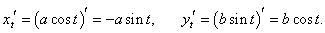 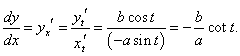 |
|
Пример 8
|
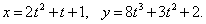
Решение.
Дифференцируем оба уравнения по параметру t:
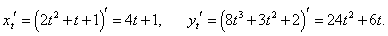 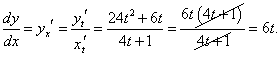 |
|
Пример 9
|
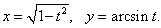
Решение.
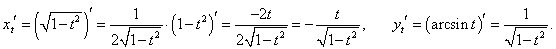 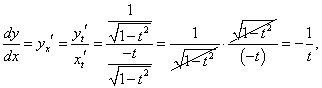 |
|
Пример 10
|
|
x = sin3 t, y = cos3 t.
Решение.
Вычислим производные xt', yt':
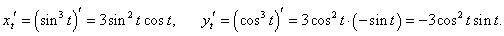 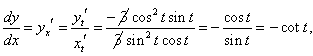 |
|
Пример 11
|
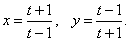
Решение.
Вычислим производные x и y по параметру t:
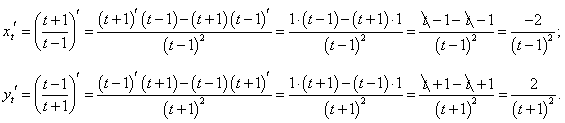 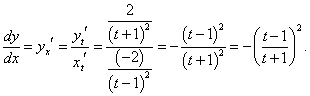 |
|
Пример 12
|
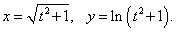
Решение.
Дифференцируя по t, находим:
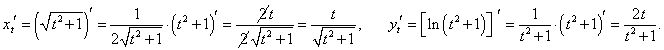 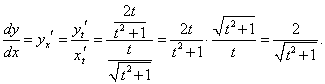 |
|
Пример 13
|
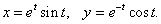
Решение.
Находим производные x и y по параметру t:
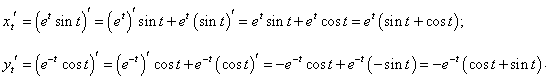 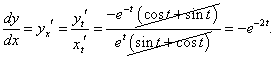 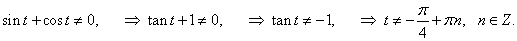 |
|
Пример 14
|
|
x = t − sin t, y = 1 − cos t.
Решение.
Производные x и y по параметру t имеют такой вид:
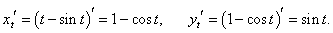 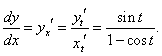 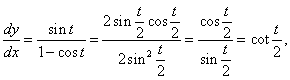 |
|
Пример 15
|
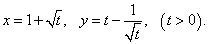
Решение.
Дифференцируем функции x(t) и y(t) по параметру t:
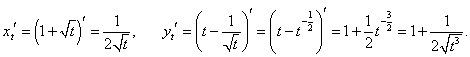 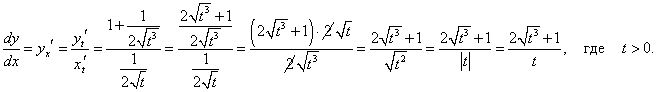 |
|
Пример 16
|
|
x = tan2 t, y = cos2 t.
Решение.
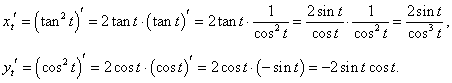 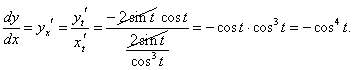 |
|
Пример 17
|
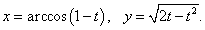
Решение.
Находим производные xt', yt':
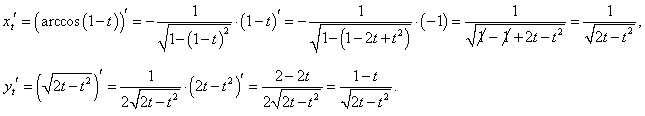 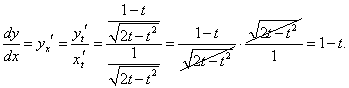 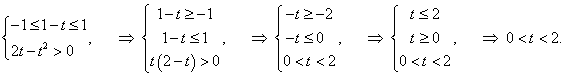 |
|
Пример 18
|
|
x = sin4 2t, y = cos4 2t.
Решение.
Производные x и y по параметру t имеют такой вид:
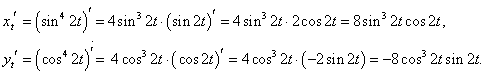 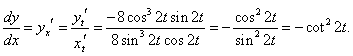 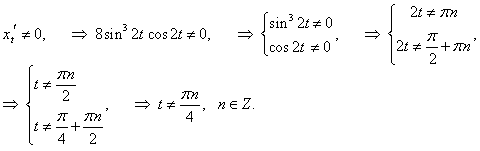 |
|
Пример 19
|
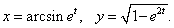
Решение.
Вычислим сначала производные x и y по переменной t:
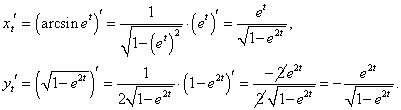 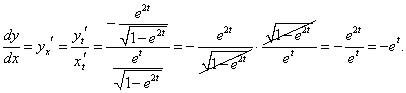 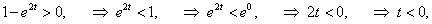 |
|
Пример 20
|
|
Найти значение производной dy/dx параметрически заданной функции x = t + 2sin πt, y = 3t − cos πt в точке t = 1/2.
Решение. 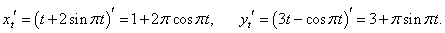 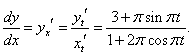 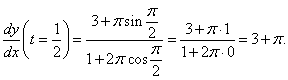 |