|
Непрерывность функций
|
||||||
|
Определение непрерывности по Гейне
Говорят, что функция действительного переменного 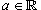 ( 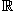 - множество действительных чисел), если для любой последовательности - множество действительных чисел), если для любой последовательности 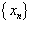 , такой, что , такой, что
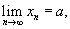 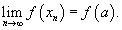
Определение непрерывности по Коши (нотация Рассмотрим функцию 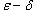 ) )
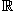 на другое подмножество B действительных чисел. Говорят, что функция на другое подмножество B действительных чисел. Говорят, что функция 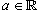 , если для любого числа , если для любого числа 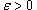 существует число существует число 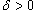 , такое, что для всех , такое, что для всех 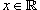 , удовлетворяющих соотношению , удовлетворяющих соотношению
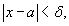 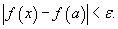
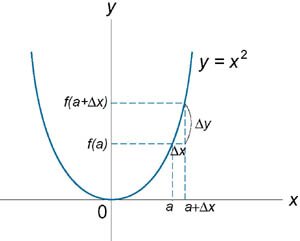
Определение непрерывности в терминах приращений аргумента и функции
Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке 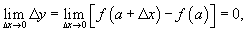 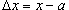 . .Приведенные определения непрерывности функции эквивалентны на множестве действительных чисел. Функция является непрерывной на данном интервале, если она непрерывна в каждой точке этого интервала.
Теоремы непрерывности
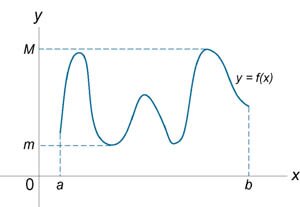
Теорема 1.Пусть функция Теорема 2. Даны две функции Теорема 3. Предположим, что две функции Теорема 4. Даны две функции 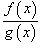 также непрерывно при также непрерывно при 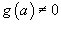 . .Теорема 5. Предположим, что функция Теорема 6 (Теорема о предельном значении). Если функция 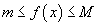
Пусть функция 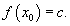
Непрерывность элементарных функций
Все элементарные функции являются непрерывными в любой точке свой области определения.Функция называется элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя:
|
||||||
|
Пример 1
|
||||||
|
Используя определение непрерывности в терминах приращений, доказать, что функция
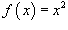 непрерывна в произвольной точке непрерывна в произвольной точке Решение. 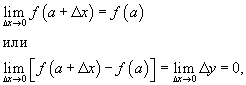 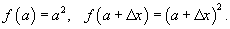 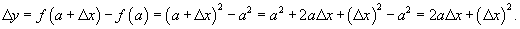 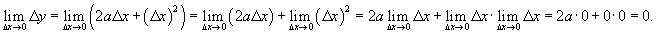
|
||||||
|
Пример 2
|
||||||
|
Используя определение непрерывности в терминах приращений, показать, что функция
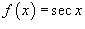 непрерывна в любой точке своей области определения. непрерывна в любой точке своей области определения.
Решение.  определена для всех действительных x, за исключением точек определена для всех действительных x, за исключением точек
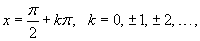 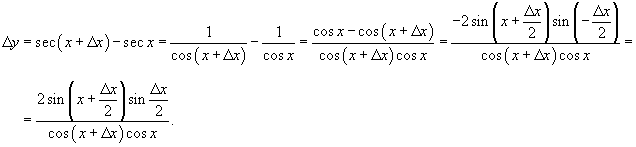  . .
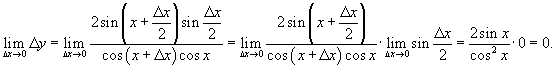 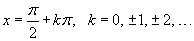 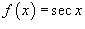 совпадают. совпадают. |
||||||
|
Пример 3
|
||||||
|
Используя определение непрерывности по Коши, доказать, что
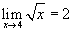 . .
Решение. 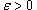 . Мы должны найти некоторое число . Мы должны найти некоторое число 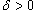 , такое, что для всех x, удовлетворяющих неравенству , такое, что для всех x, удовлетворяющих неравенству
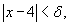 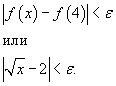 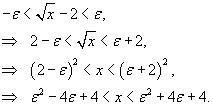 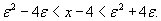  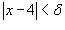 , получим , получим 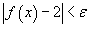 . Например, если . Например, если 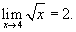 |
||||||
|
Пример 4
|
||||||
|
Показать, что кубическое уравнение
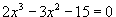 имеет решение в интервале (2,3). имеет решение в интервале (2,3).
Решение. 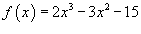 . Вычислим значения функции при . Вычислим значения функции при 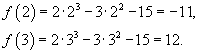 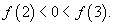 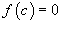 . Таким образом, данное уравнение имеет решение в интервале (2,3). . Таким образом, данное уравнение имеет решение в интервале (2,3). |
||||||
|
Пример 5
|
||||||
|
Показать, что уравнение
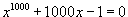 имеет, по крайней мере, один корень. имеет, по крайней мере, один корень.
Решение. 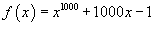 является полиномом, то она непрерывна. Заметим, что является полиномом, то она непрерывна. Заметим, что
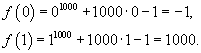  . По теореме о промежуточном значении можно сделать вывод, что в интервале (0,1) существует число c, такое, что . По теореме о промежуточном значении можно сделать вывод, что в интервале (0,1) существует число c, такое, что 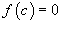 . Таким образом, уравнение имеет корень в интервале (0,1). . Таким образом, уравнение имеет корень в интервале (0,1). |
||||||
|
Пример 6
|
||||||
|
Задана функция
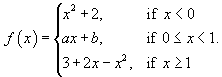 Решение. 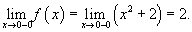 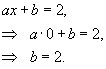 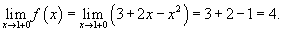 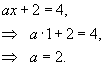 |
||||||
|
Пример 7
|
||||||
|
Если функция
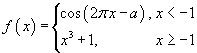 Решение. 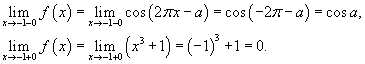 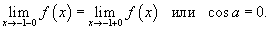 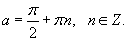 |
||||||
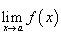 существует;
существует;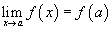 .
.
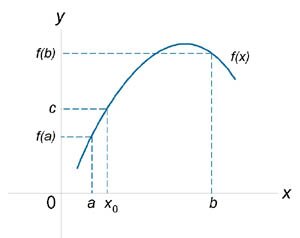
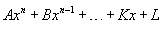 ;
;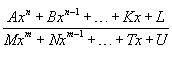 ;
;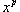 ;
;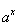 ;
;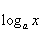 ;
;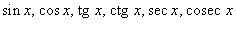 ;
;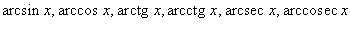 ;
;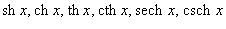 ;
; .
.