|
Уравнение Эйлера высшего порядка
|
|
Уравнение Эйлера n-го порядка записывается в виде
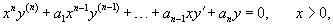 Ранее мы уже рассматривали уравнения Эйлера второго порядка. С помощью определенных подстановок такое уравнение сводится к линейному однородному дифференциальному уравнению с постоянными коэффициентами. Такие преобразования используются и в случае уравнения n-го порядка. Рассмотрим подробнее два метода решения уравнений данного вида.
1. Решение уравнения Эйлера n-го порядка с помощью подстановки x = exp(t)
Используя подстановку 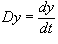 . Таким образом, мы получаем: . Таким образом, мы получаем:
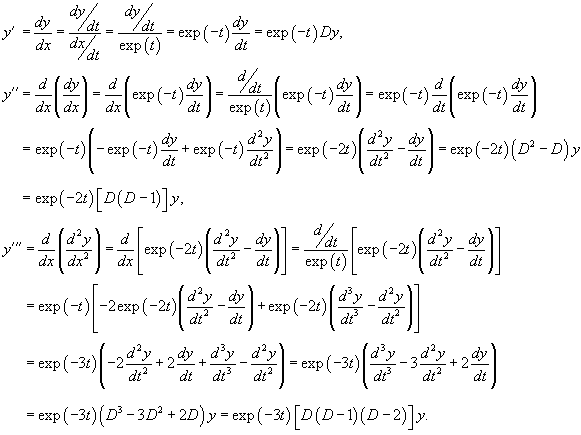 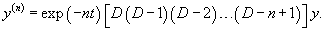 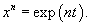
2. Решение уравнения Эйлера n-го порядка в виде степенной функции y = x k
Рассмотрим другой способ решения уравнения Эйлера. Предположим, что решение имеет вид степенной функции 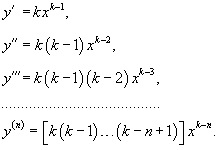 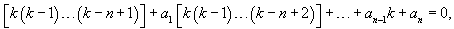 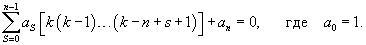
3. Неоднородное уравнение Эйлера высшего порядка
В общем случае неоднородное уравнение Эйлера представляется в виде
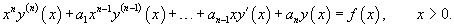 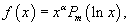 |
|
Пример 1
|
|
Найти общее решение уравнения
Решение. 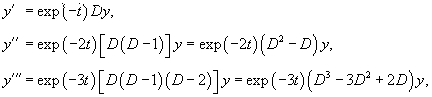 Подставляя выражения для производных и учитывая, что 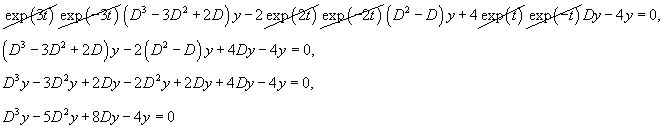 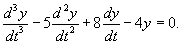 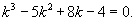 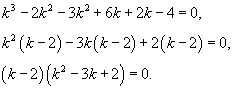 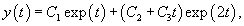 Перейдем обратно от переменной t к x, учитывая, что 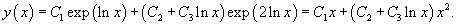 |
|
Пример 2
|
|
Найти общее решение уравнения
Решение. 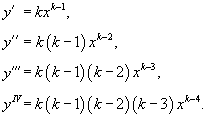 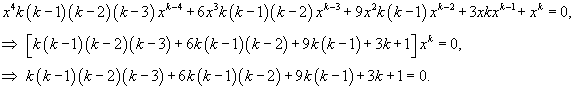 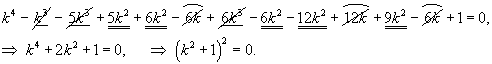 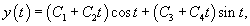 Сделаем обратную подстановку 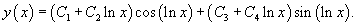 |
|
Пример 3
|
|
Решить дифференциальное уравнение
Решение. 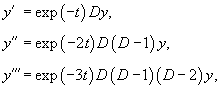 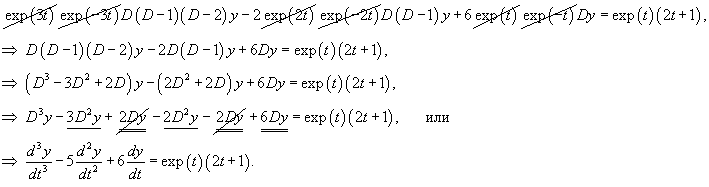 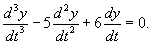 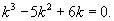 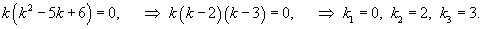 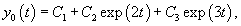 Теперь определим частное решение неоднородного уравнения. Заметим, что экспоненциальная функция   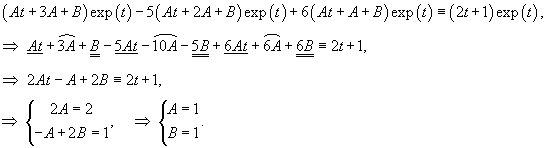 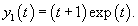 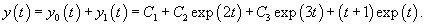 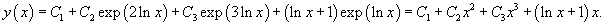 |