|
Уравнение Эйлера второго порядка
|
|
Линейное дифференциальное уравнение второго порядка вида
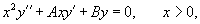
Первый способ решения уравнения Эйлера
Сделаем следующую подстановку: 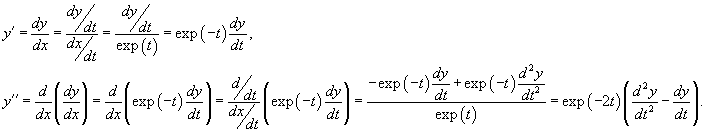 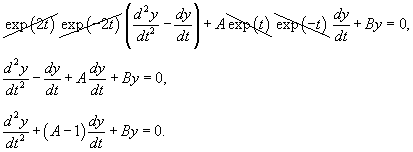 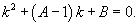 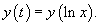
Второй способ решения уравнения Эйлера
В рамках второго способа мы ищем решение уравнения в форме степенной функции 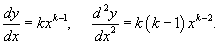 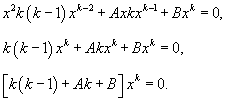 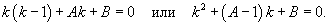
Неоднородное уравнение Эйлера
Неоднородное уравнение Эйлера записывается в виде:
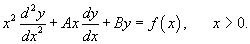 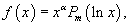
|
|
Пример 1
|
|
Найти общее решение дифференциального уравнения
Решение. 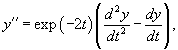 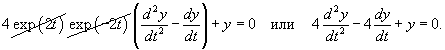 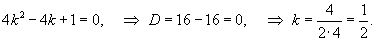 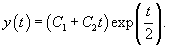 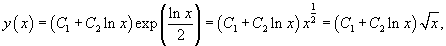 |
|
Пример 2
|
|
Найти общее решение дифференциального уравнения
Решение. 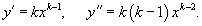 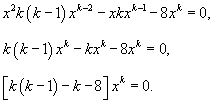 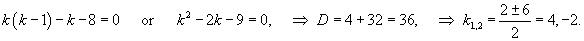 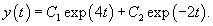 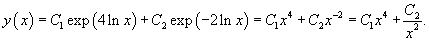 |
|
Решение 3
|
|
Найти общее решение уравнения Эйлера
Решение. 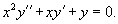 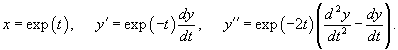 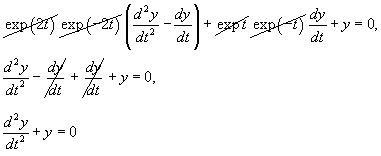 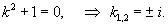 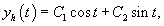 Теперь определим частное решение неоднородного уравнения 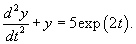 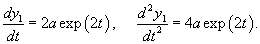  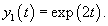 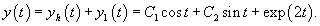 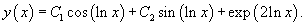 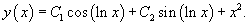 |
|
Пример 4
|
|
Решить неоднородное уравнение Эйлера
Решение. 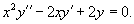 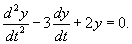 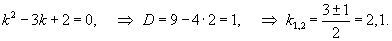 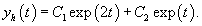 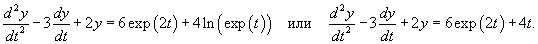 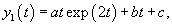 Первая и вторая производные данной функции будут равны 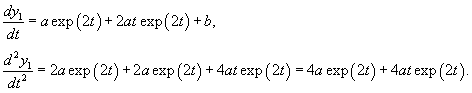 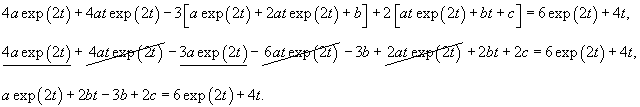 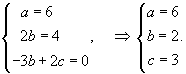 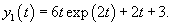 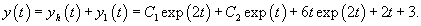 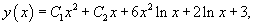 |