|
Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
|
|
|
Рассмотрим линейное дифференциальное уравнение вида
 Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение: 
|
|
|
Пример 1
|
|
|
Решить дифференциальное уравнение
Решение.   |
|
|
Пример 2
|
|
|
Найти общее решение дифференциального уравнения
Решение.   |
|
|
Пример 3
|
|
|
Решить дифференциальное уравнение
Решение.   |
|
|
Пример 4
|
|
|
Решить уравнение
Решение. 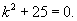 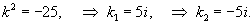 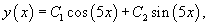 |
|
|
Пример 5
|
|
|
Решить уравнение
Решение. 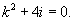 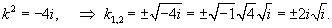 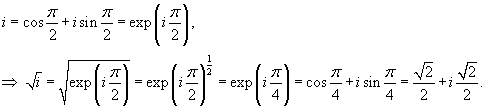 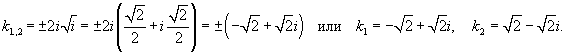 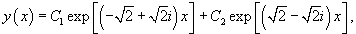 |
|



