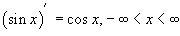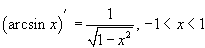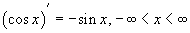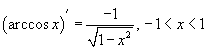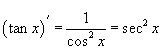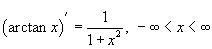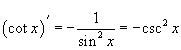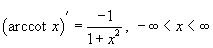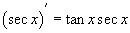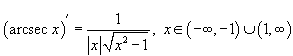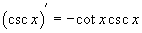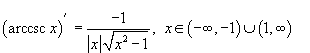|
Производные тригонометрических функций
|
||||||||||||
|
К основным тригонометрическим функциям относятся следующие 6 функций: синус (sin x), косинус (cos x), тангенс (tg x или tan x), котангенс (ctg x или cot x), секанс (sec x) и косеканс (csc x).
Для каждой из этих функций существует обратная тригонометрическая функция. Они называются, соответственно, арксинус (arcsin x), арккосинус (arccos x), арктангенс (arctg x или arctan x), арккотангенс (arcctg x или arccot x), арксеканс (arcsec x) и арккосеканс (arccsc x). Все указанные функции непрерывны и дифференцируемы в своей области определения. Далее мы составим список производных для этих 12 функций.
Производные основных тригонометрических функций
На странице Определение производной мы уже вывели производные для синуса и косинуса. Они имеют следующий вид:
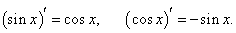 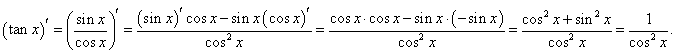 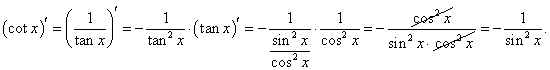 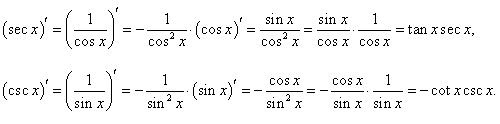
Производные обратных тригонометрических функций
Производные обратных тригонометрических функций можно вывести, используя теорему о производной обратной функции. Так, например, для функции y = f (x) = arcsin x обратной функцией является синус, т.е. x = φ (y) = sin y. Тогда производная арксинуса равна:
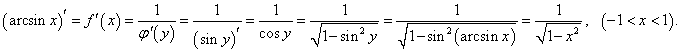  Аналогично определяется производная арккосеканса: 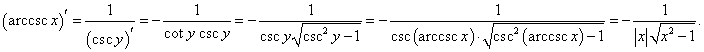
Таблица производных тригонометрических функций
Рассмотренные производные 6 основных тригонометрических функций и 6 обратных тригонометрических функций представлены в следующей таблице:
|
||||||||||||
|
Пример 1
|
||||||||||||
|
y = cos2x − 2sinx.
Решение.
Используя линейные свойства производной, правило дифференцирования сложной функции и формулу двойного угла, получаем:
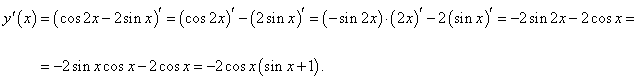 |
||||||||||||
|
Пример 2
|
||||||||||||
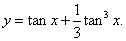
Решение.
Производная данной функции имеет следующий вид:
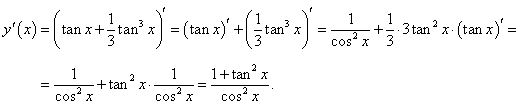 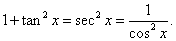 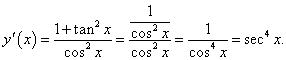 |
||||||||||||
|
Пример 3
|
||||||||||||
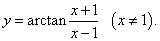
Решение.
Используя формулы производной сложной функции и производной частного, получаем:
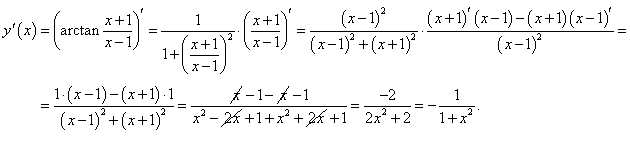 |
||||||||||||
|
Пример 4
|
||||||||||||
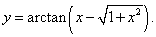
Решение.
Применяем дважды правило дифференцирования сложной функции и упрощаем полученное выражение:
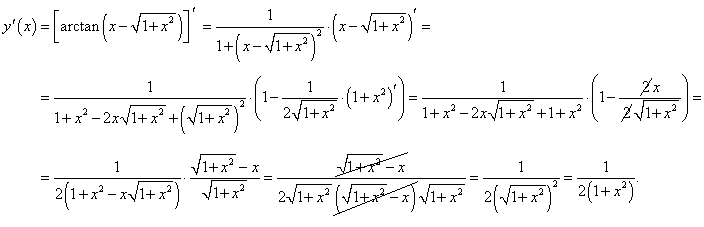 |
||||||||||||
|
Пример 5
|
||||||||||||
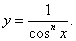
Решение.
Найдем производную данной функции, используя правила дифференцирования степенной функции и сложной функции:
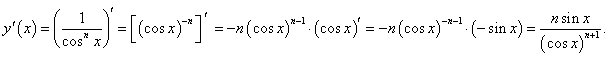 |
||||||||||||
|
Пример 6
|
||||||||||||
|
y = cos2 sin x.
Решение.
Применяя правила дифференцирования степенной функции и сложной функции, получаем:
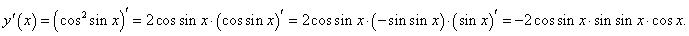 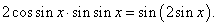 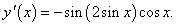 |
||||||||||||
|
Пример 7
|
||||||||||||
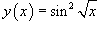
Решение.
Применим правило производной сложной функции несколько раз.
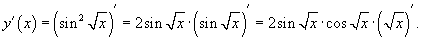 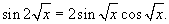 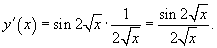 |
||||||||||||
|
Пример 8
|
||||||||||||
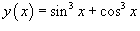
Решение.
Используем формулы для производной суммы функций и производной степенной функции.
 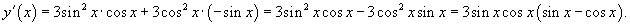 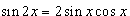 , то окончательное выражение для производной имеет вид , то окончательное выражение для производной имеет вид
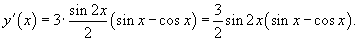 |
||||||||||||
|
Пример 9
|
||||||||||||
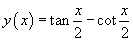
Решение.
Первый шаг очевиден:
 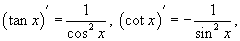 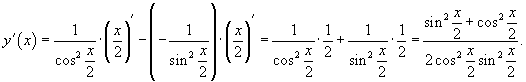  и и 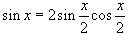 , получаем ответ: , получаем ответ:
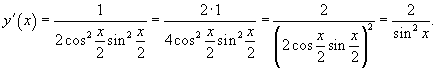 |
||||||||||||
|
Пример 10
|
||||||||||||
|
Вывести формулу для производной арксинуса с помощью производной сложной функции.
Решение.  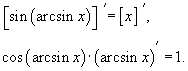 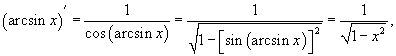 |
||||||||||||
|
Пример 11
|
||||||||||||
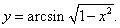
Решение.
По правилу дифференцирования сложной функции имеем
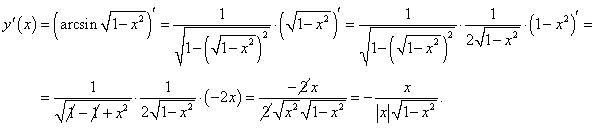 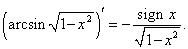 |
||||||||||||
|
Пример 12
|
||||||||||||
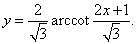
Решение.
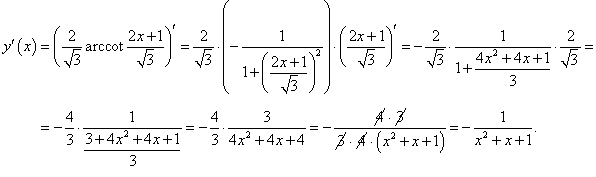 |
||||||||||||
|
Пример 13
|
||||||||||||
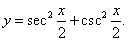
Решение.
Применяя линейные свойства производной и правило дифференцирования сложной функции, получаем:
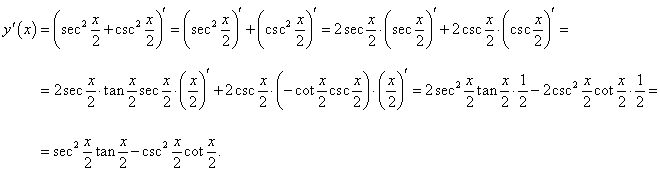 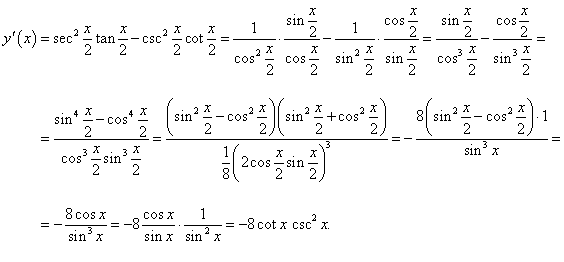 |
||||||||||||
|
Пример 14
|
||||||||||||
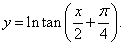
Решение.
Здесь предполагается, что значения x удовлетворяют области определения функции, которая находится из решения неравенства:
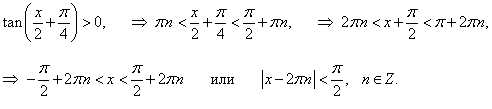 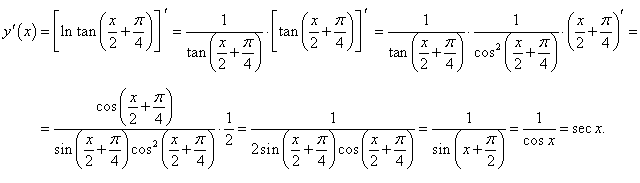 |
||||||||||||
|
Пример 15
|
||||||||||||
|
y = sinn x cos nx.
Решение.
Сначала дифференцируем как произведение двух функций:
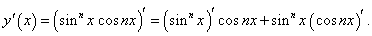 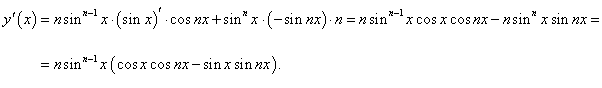 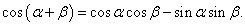 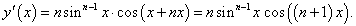 |
||||||||||||
|
Пример 16
|
||||||||||||
|
Показать, что
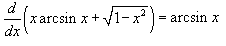 . .
Решение. 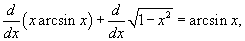 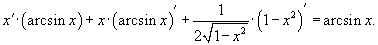 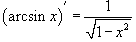 , получаем: , получаем:
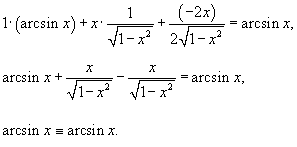 |
||||||||||||
|
Пример 17
|
||||||||||||
|
y = (tan x)cos x, где 0 < x < π/2.
Решение.
Представим данную функцию таким образом:
 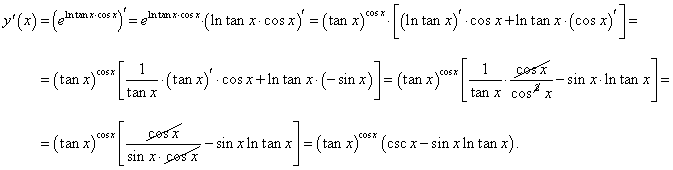 |
||||||||||||
|
Пример 18
|
||||||||||||
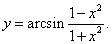
Решение.
Заметим, что функция арксинус определена на отрезке [−1, 1]. В нашем случае условие, определяющее допустимые значения x, выглядит так:
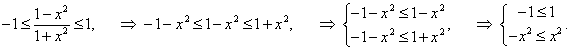 Вычислим производную, используя правило дифференцирования сложной функции: 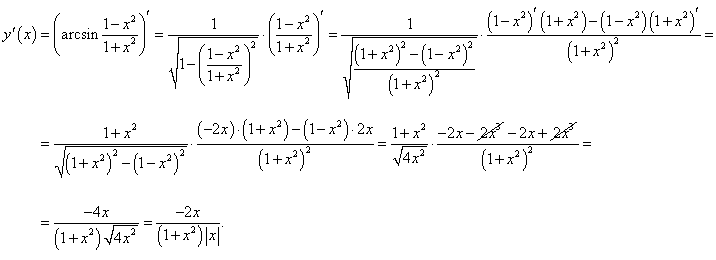 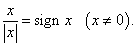 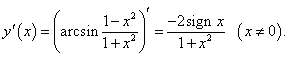 |
||||||||||||
|
Пример 19
|
||||||||||||
|
y = sin(cos2 x)⋅cos(sin2 x).
Решение.
По формуле произведения двух функций:
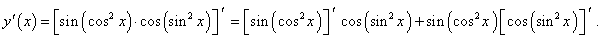 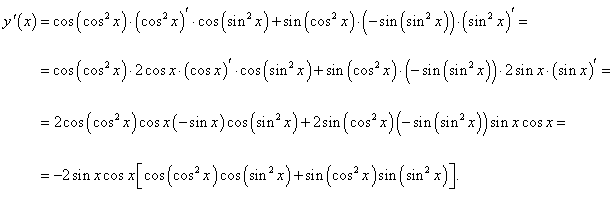 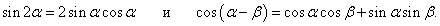 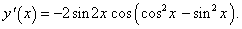 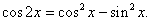 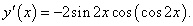 |
||||||||||||
|
Пример 20
|
||||||||||||
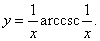
Решение.
Начнем вычисление производной по формуле производной произведения:
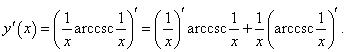 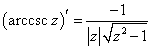 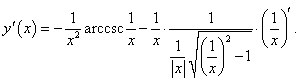 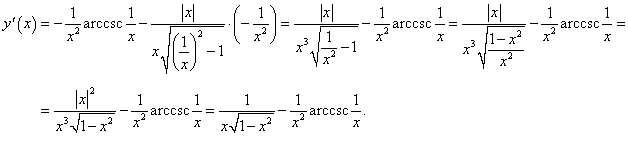 |
||||||||||||