|
Производная степенной функции
|
|
Если
 Если показатель степени является отрицательным числом, т.е. 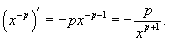 Производная полинома  . Тогда . Тогда
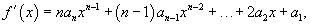 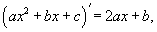
Производная иррациональной функции
Если 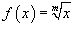 , то такую функцию можно представить как степенную с показателем 1/m. Ее производная равна , то такую функцию можно представить как степенную с показателем 1/m. Ее производная равна
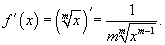 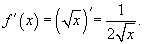 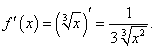 |
|
Пример 1
|
|
Вычислить производную функции
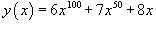 . .
Решение. 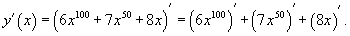 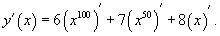 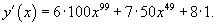 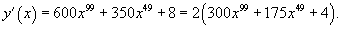 |
|
Пример 2
|
|
Вычислить производную функции
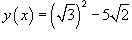 . .
Решение. 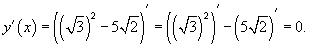 |
|
Пример 3
|
|
Найти производную функции
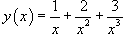 . .
Решение. 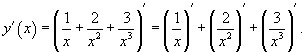 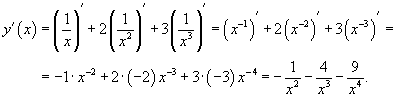 |
|
Пример 4
|
|
Найти производную следующей функции
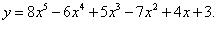
Решение. 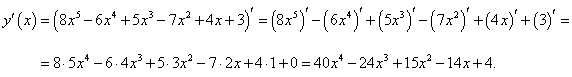 |
|
Пример 5
|
|
Найти производную функции
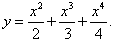
Решение. 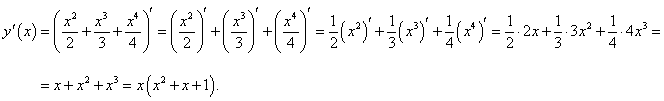 |
|
Пример 6
|
|
Найти производную функции
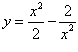 . .
Решение. 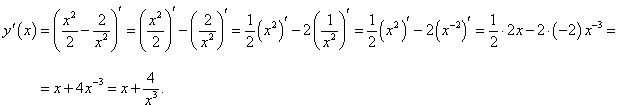 |
|
Пример 7
|
|
Вычислить значение производной функции
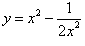 в точке в точке
Решение.
Производная данной функции имеет вид:
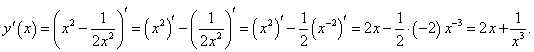 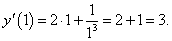 |
|
Пример 8
|
|
Найти производную функции
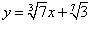 . .
Решение. 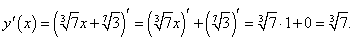 |
|
Пример 9
|
|
Найти производную функции
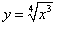 . .
Решение. 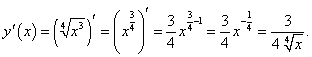 |
|
Пример 10
|
|
Найти производную иррациональной функции
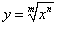 , где , где Решение. 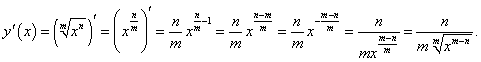 |
|
Пример 11
|
|
Вычислить производную функции
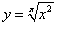 . .
Решение. 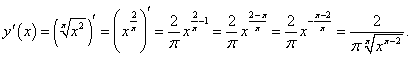 |
|
Пример 12
|
|
Найти производную следующей функции:
 . .
Решение. 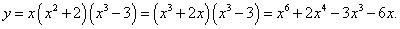 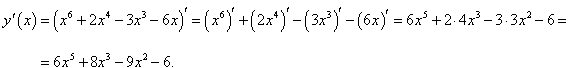 |
|
Пример 13
|
|
Вычислить производную функции
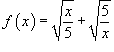 . .
Решение. 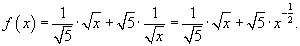 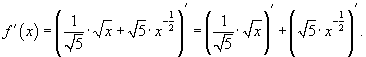 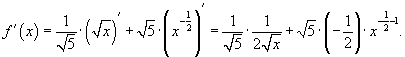 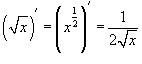 . После упрощения получаем . После упрощения получаем
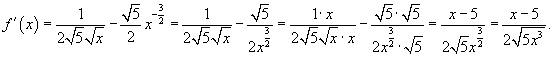 |
|
Пример 14
|
|
Найти производную функции
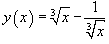 . .
Решение. 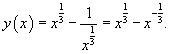 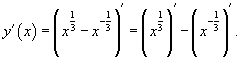 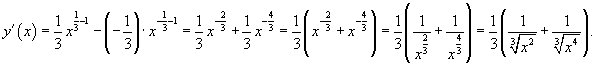 |
|
Пример 15
|
|
Найти производную функции
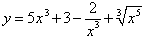 . .
Решение. 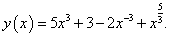 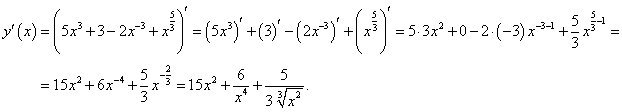 |
|
Пример 16
|
|
Найти производную функции
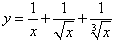 . .
Решение. 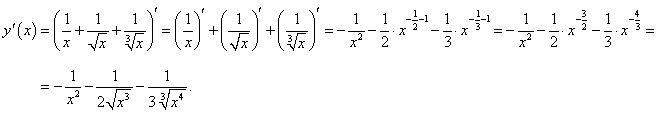 |
|
Пример 17
|
|
Вычислить производную функции
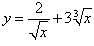 . .
Решение. 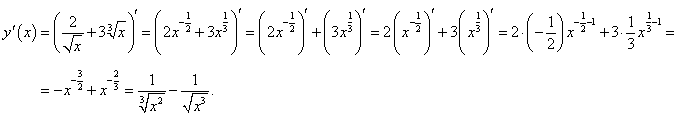 |
|
Пример 18
|
|
Найти производную иррациональной функции
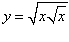 . .
Решение. 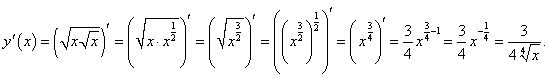 |
|
Пример 19
|
|
Найти производную следующей иррациональной функции
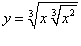 . .
Решение. 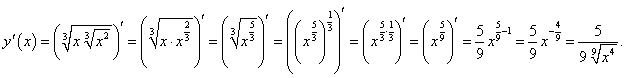 |
|
Пример 20
|
|
Найти производную функции
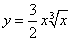 . .
Решение. 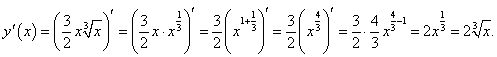 |