|
Производная произведения и частного функций
|
|
Производная произведения функций
Пусть  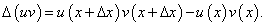 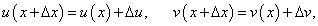 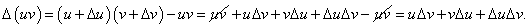 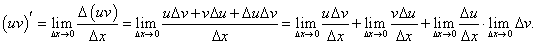 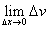 : :
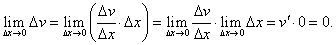 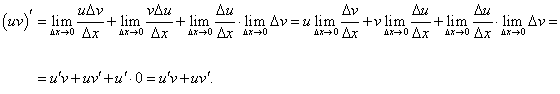 Производная произведения двух функций НЕ РАВНА произведению производных этих функций! Из данной формулы легко получить выражение для производной функции 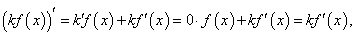
Производная частного функций
Пусть 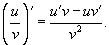 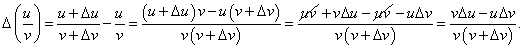 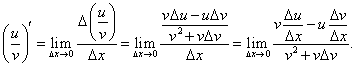 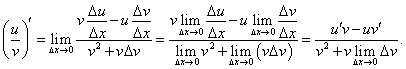 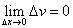 , получаем окончательное выражение для производной частного двух функций: , получаем окончательное выражение для производной частного двух функций:
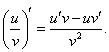 |
|
Пример 1
|
|
Найти производную функции
Решение. 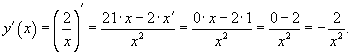 |
|
Пример 2
|
|
Найти производную cтепенной функции с отрицательным показателем
Решение. 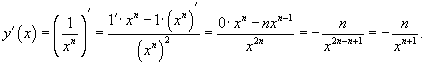 |
|
Пример 3
|
|
Вычислить производную
Решение. 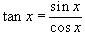 . Тогда . Тогда
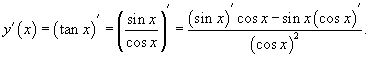 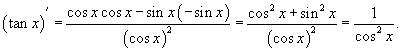 |
|
Пример 4
|
|
Пусть
Решение. 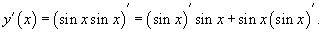 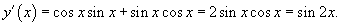 |
|
Пример 5
|
|
Найти производную функции
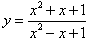 . .
Решение. 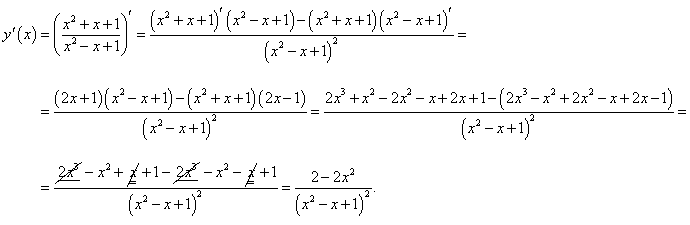 |
|
Пример 6
|
|
Найти производную функции секанс
Решение. 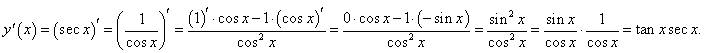 |
|
Пример 7
|
|
Найти производную функции
Решение. 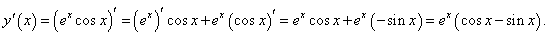 |
|
Пример 8
|
|
Найти производную функции
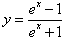 и вычислить ее значение при и вычислить ее значение при Решение. 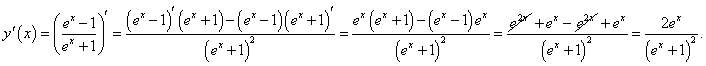 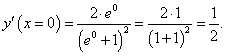 |
|
Пример 9
|
|
Найти производную функции
Решение. 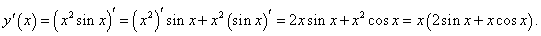 |
|
Пример 10
|
|
Дана функция
Решение. 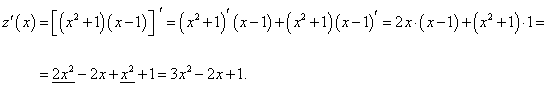 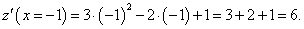 |
|
Пример 11
|
|
Найти формулу для производной произведения трех функций.
Решение. 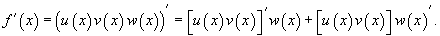  |
|
Пример 12
|
|
Найти производную функции
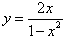 . .
Решение. 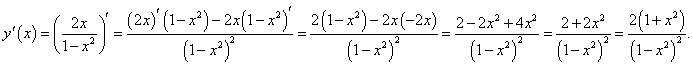 |
|
Пример 13
|
|
Вычислить производную функции
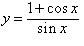 . .
Решение. 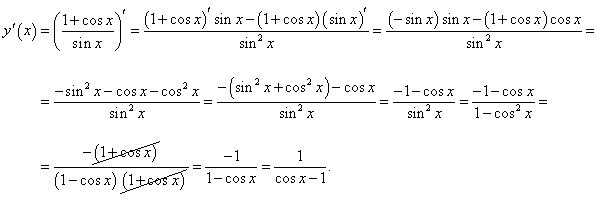 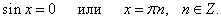 |
|
Пример 14
|
|
Продифференцировать функцию
Решение. 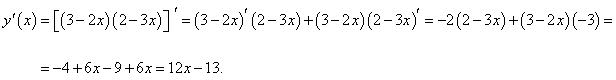 |
|
Пример 15
|
|
Продифференцировать функцию
Решение. 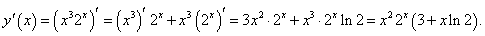 |
|
Пример 16
|
|
Найти производную дробно-линейной функции
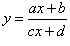 . .
Решение. 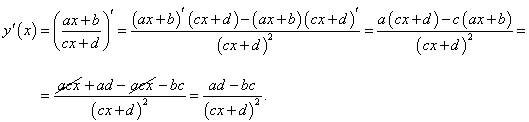 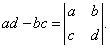 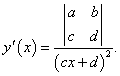 |
|
Пример 17
|
|
Вычислить производную функции
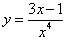 . .
Решение. 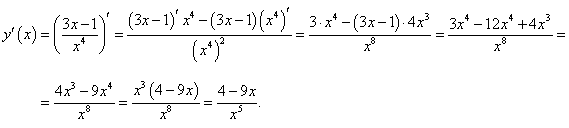 |
|
Пример 18
|
|
Найти производную функции
Решение. 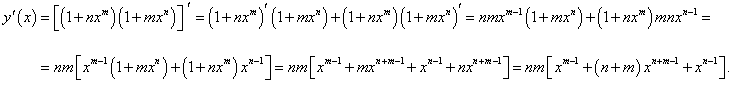 |
|
Пример 19
|
|
Вычислить производную следующей функции:
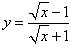 . .
Решение. 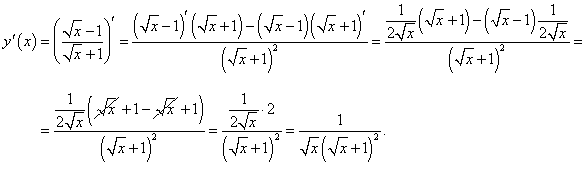 |
|
Пример 20
|
|
Вывести формулу производной функции
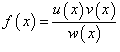 . .
Решение. 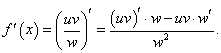 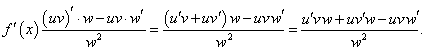 |