|
Простейшие правила дифференцирования
|
|
Операция дифференцирования или нахождения производной функции обладает фундаментальным свойством линейности. Это свойство упрощает нахождение производных функций, которые образованы из основных элементарных функций с помощью операций сложения и умножения на постоянное число. Простейшие правила дифференцирования позволяют вычислять производные таких функций без использования формального определения производной. Рассмотрим эти правила более подробно.
Производная постоянной величины. 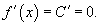 Производная функции, умноженной на постоянную величину. 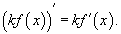 Производная суммы функций. 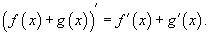 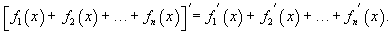 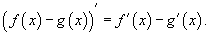
Производная линейной комбинации функций.
Предположим, что 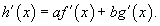
Производная функции y = x.
Если 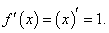 |
|
Пример 1
|
|
Найти производную функции
Решение. 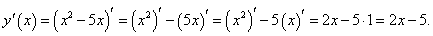 |
|
Пример 2
|
|
Найти производную функции
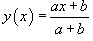 , где a и b - константы. , где a и b - константы.
Решение. 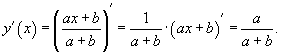 |
|
Пример 3
|
|
Найти производную функции 2√x − 3sin x.
Решение. 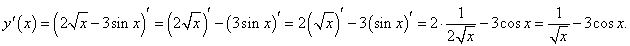 |
|
Пример 4
|
|
Найти производную функции
Решение. 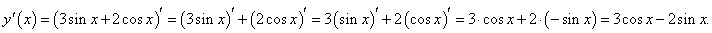 |
|
Пример 5
|
|
Пусть
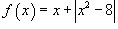 . Найти производную функции в точке . Найти производную функции в точке Решение. 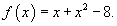 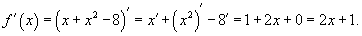 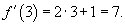 |
|
Пример 6
|
|
Найти производную функции
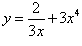 . .
Решение.
Применяя линейные свойства производной, получаем следующий ответ:
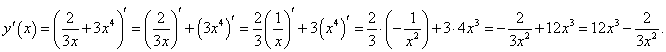 |
|
Пример 7
|
|
Найти производную функции
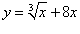 . .
Решение. 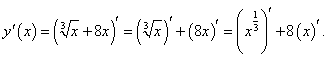 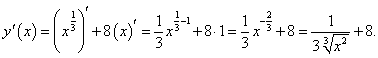 |
|
Пример 8
|
|
Вычислить производную следующей функции
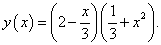
Решение.
Чтобы решить данный пример с помощью рассмотренных выше правил дифференцирования, перемножим обе скобки и запишем функцию в таком виде:
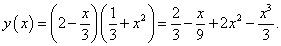 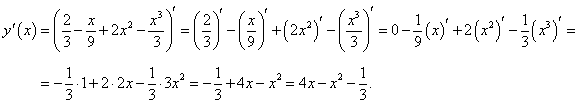 |
|
Пример 9
|
|
Вычислить производную функции
Решение.
Раскрывая скобки, запишем заданную функцию как
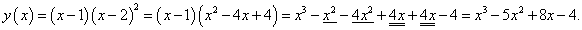 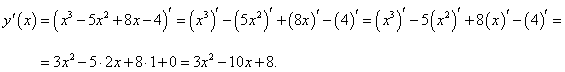 |
|
Пример 10
|
|
Найти производную функции
 , не используя формулу производной частного. , не используя формулу производной частного.
Решение.
Разделив числитель на знаменатель почленно, запишем функцию в виде
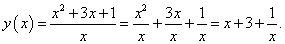 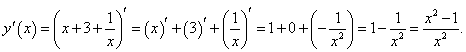 |