|
Уравнение Риккати
|
|
Общее уравнение Риккати
Уравнение Риккати является одним из наиболее интересных нелинейных дифференциальных уравнений первого порядка. Оно записывается в форме:
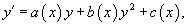 Уравнение Риккати встречается в различных областях математики (например, в алгебраической геометрии и в теории конформных отображений) и физики. Оно также нередко возникает в прикладных математических задачах. Приведенное выше уравнение называется общим уравнением Риккати. Его решение основано на следующей теореме: Теорема: Если известно частное решение y1 уравнения Риккати, то его общее решение определяется формулой 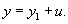 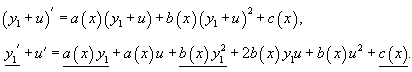 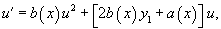 Помимо общего уравнения Риккати, существует множество частных случаев уравнения Риккати с коэффициентами Возвращаясь вновь к общему уравнению Риккати, мы видим, что общее решение можно сконструировать, если известно какое-либо частное решение. К сожалению, не существует строгого алгоритма для нахождения частного решения, которое существенно зависит от вида функций Ниже мы рассмотрим некоторые хорошо известные частные случаи уравнения Риккати.
Частный случай 1: Коэффициенты a, b, c − константы.
Если коэффициенты в уравнении Риккати постоянны, то такое уравнение можно привести к уравнению с разделяющимися переменными. В этом случае общее решение описывается интегралом от рациональной функции с квадратичным трехчленом в знаменателе:
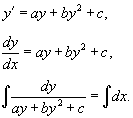
Частный случай 2: Уравнение вида Рассмотрим уравнение Риккати вида 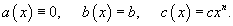 Прежде всего, заметим, что если Если Данное дифференциальное уравнение можно также решить при 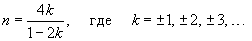 При всех других значениях степени n решение уравнения Риккати можно выразить через интегралы от элементарных функций. Этот факт был установлен французским математиком Джозефом Лиувиллем (1809-1882) в 1841 году. Многие другие частные случаи уравнения Риккати представлены на сайте EqWorld. |
|
Пример 1
|
|
Решить дифференциальное уравнение
Решение. 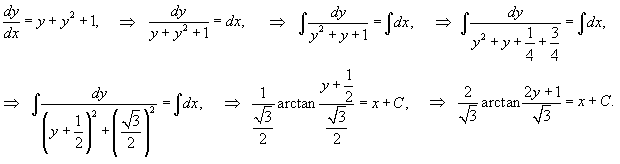 |
|
Пример 2
|
|
Решить уравнение Риккати
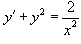 . .
Решение. 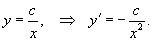 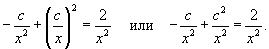 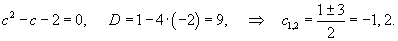 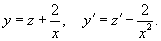 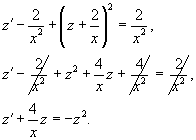 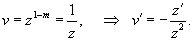 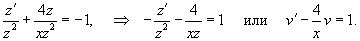 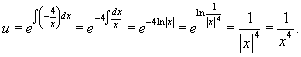 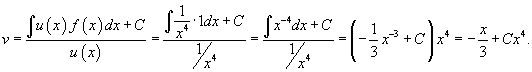 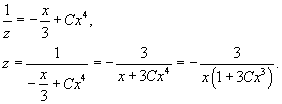 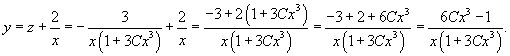 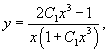 |
|
Пример 3
|
|
Найти общее решение дифференциального уравнения
Решение. 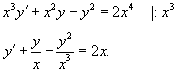 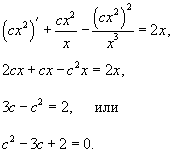 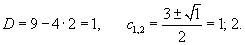 В результате можно записать общее решение уравнения Риккати в форме: 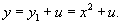 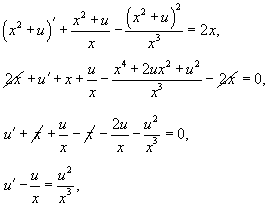 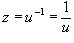 преобразует его в линейное дифференциальное уравнение: преобразует его в линейное дифференциальное уравнение:
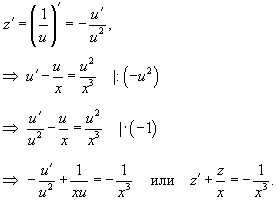 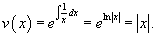 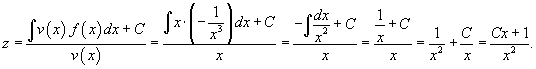 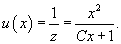 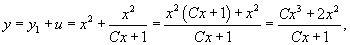 |
|
Пример 4
|
|
Решить уравнение
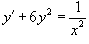 . .
Решение. Сделав подстановку Пусть 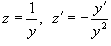 . Тогда . Тогда
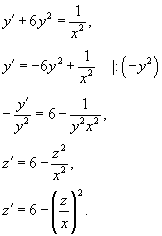 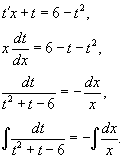 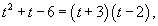 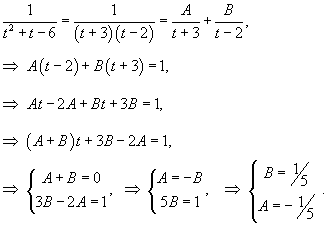 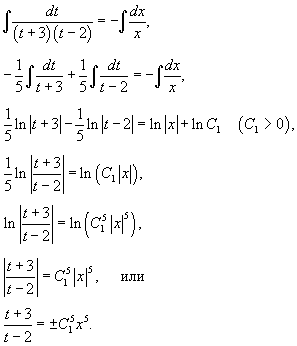 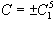 , так что решение для функции , так что решение для функции 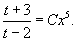 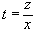 . Поэтому . Поэтому
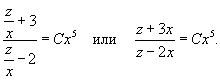 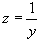 , находим: , находим:
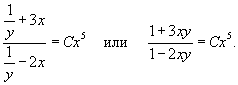 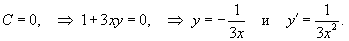 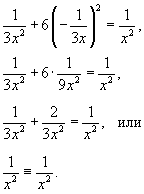 |