|
Уравнение Бернулли
|
|
Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде
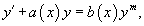 Если В общем случае, когда 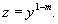 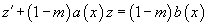 |
|
Пример 1
|
|
Найти общее решение уравнения
Решение. 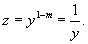 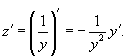 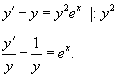 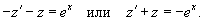 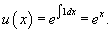 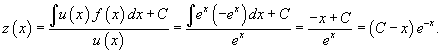 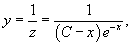 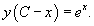 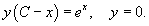 |
|
Пример 2
|
|
Решить дифференциальное уравнение
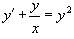 . .
Решение. 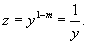 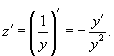 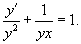 Дифференциальное уравнение для новой переменной z имеет вид:  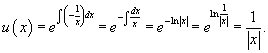 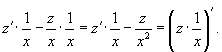 Тогда общее решение линейного дифференциального уравнения для функции 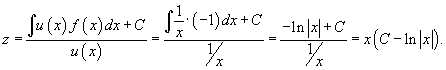 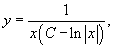 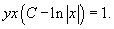  |
|
Пример 3
|
|
Найти все решения дифференциального уравнения
Решение. 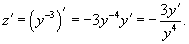 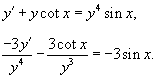 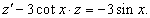 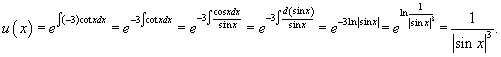  . После умножения на . После умножения на 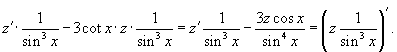 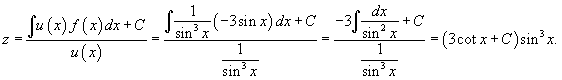 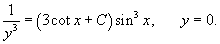 |
|
Пример 4
|
|
Найти все решения дифференциального уравнения
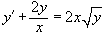 . .
Решение. 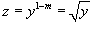 . Производная новой функции . Производная новой функции 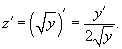 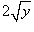 . Аналогично другим примерам на этой веб-странице, корень . Аналогично другим примерам на этой веб-странице, корень 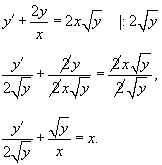 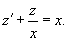 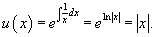  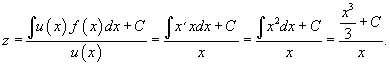 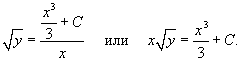 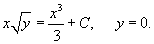 |
|
Пример 5
|
|
Найти решение дифференциального уравнения
Решение. 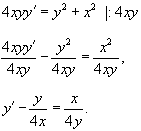 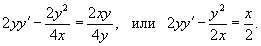 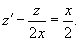 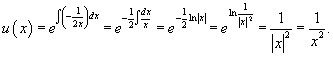 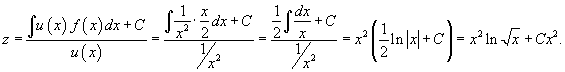 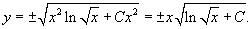 Видно, что только решение с положительным знаком удовлетворяет данному условию. Следовательно, 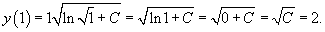 Итак, решение задачи Коши выражается функцией  |