|
Линейные дифференциальные уравнения первого порядка
|
|
Определение линейного уравнения первого порядка
Дифференциальное уравнение вида
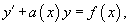
Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
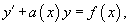 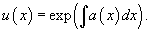 Общее решение диффференциального уравнения выражается в виде: 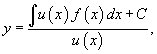
Метод вариации постоянной
Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
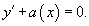 Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.
Задача Коши
Если, кроме дифференциального уравнения, задано также начальное условие в форме Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие |
|
Пример 1
|
|
Решить уравнение
Решение. 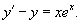 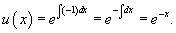 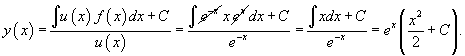 |
|
Пример 2
|
|
Решить дифференциальное уравнение
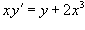 . .
Solution. 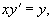 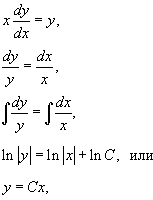 Теперь заменим константу C на некоторую (пока неизвестную) функцию 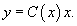 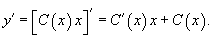 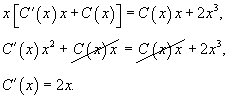 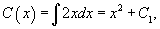 Таким образом, общее решение заданного уравнения записывается в виде: 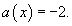 |
|
Пример 3
|
|
Решить уравнение
Решение. 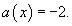 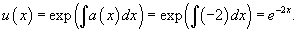 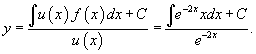 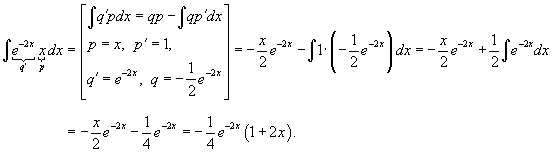 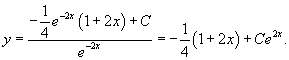 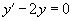 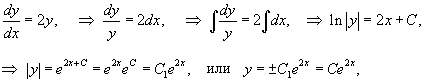 Далее предположим, что C является функцией x и подставим решение 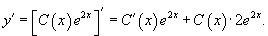 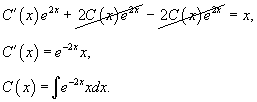 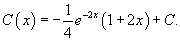 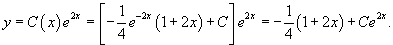 |
|
Пример 4
|
|
Решить дифференциальное уравнение
Решение. 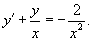 Рассмотрим однородное уравнение: 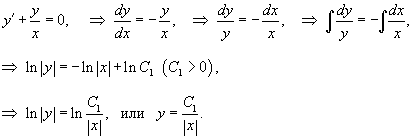 Теперь заменим константу C на функцию 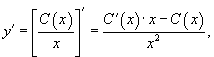 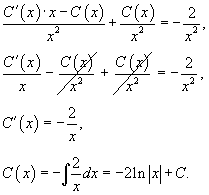 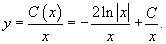 |
|
Пример 5
|
|
Решить задачу Коши:
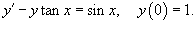
Решение. 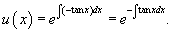 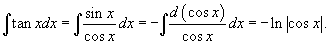 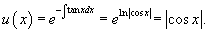 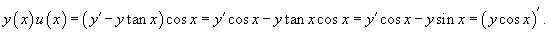 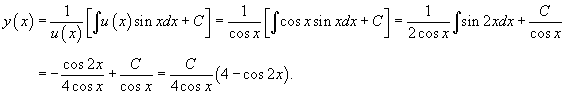 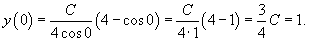 Следовательно, решение задачи Коши выражается формулой: 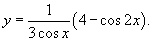 |
|
Пример 6
|
|
Решить дифференциальное уравнение (задачу Коши)
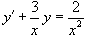 с начальным условием с начальным условием Решение. 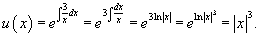 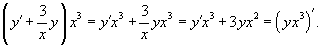 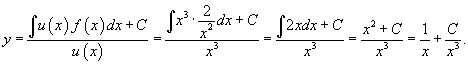 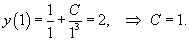 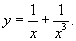 |
|
Пример 7
|
|
Найти общее решение дифференциального уравнения
Решение. 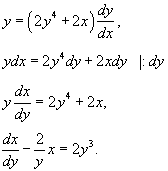 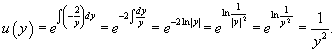 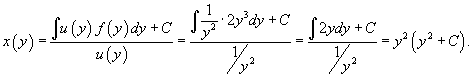 |