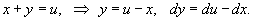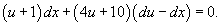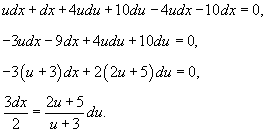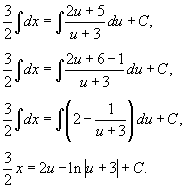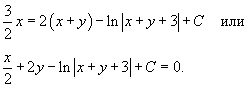|
|
|
|
Уравнения с разделяющимися переменными
|
|
Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:
где p(x) и h(y) − непрерывные функции.
Рассматривая производную y' как отношение дифференциалов 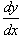 , перенесем dx в правую часть и разделим уравнение на h(y):
Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x0, при котором h(x0) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.
Обозначив 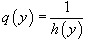 , запишем уравнение в форме:
Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:
где C − постоянная интегрирования.
Вычисляя интегралы, получаем выражение
описывающее общее решение уравнения с разделяющимися переменными.
|
|
Пример 1
|
|
Решить дифференциальное уравнение 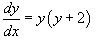 .
Решение.
В данном случае p(x) = 1 и h(y) = y(y +2). Разделим уравнение на h(y) и перенесем dx в правую часть:
Заметим, что при делении мы могли потерять решения y = 0 и y = −2 в случае когда h(y) равно нулю. Действительно, убедимся, что y = 0 является решением данного дифференциального уравнения. Пусть
Подставляя это в уравнение, получаем: 0 = 0. Следовательно, y = 0 будет являться одним из решений. Аналогично можно проверить, что y = −2 также является решением уравнения.
Вернемся обратно к дифференциальному уравнению и проинтегрируем его:
Интеграл в левой части можно вычислить методом неопределенных коэффициентов:
Таким образом, мы получаем следующее разложение рациональной дроби в подыинтегральном выражении:
Следовательно,
Переименуем константу: 2C = C1. В итоге, окончательное решение уравнения записывается в виде:
Общее решение здесь выражено в неявном виде. В данном примере мы можем преобразовать его и получить ответ в явной форме в виде функции y = f(x,C1), где C1 − некоторая константа. Однако это можно сделать не для всех дифференциальных уравнений.
|
|
Пример 2
|
|
Решить дифференциальное уравнение 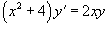 .
Solution.
Запишем данное уравнение в следующем виде:
Разделим обе части на (x2 + 4)y:
Очевидно, что x2 + 4 ≠ 0 для всех действительных x. Проверим, что y = 0 является одним из решений уравнения. После подстановки y = 0 и dy = 0 в исходное дифференциальное уравнение видно, что функция y = 0 действительно является решением уравнения.
Теперь можно проинтегрировать полученное уравнение:
Заметим, что dx2 = d(x2 + 4). Следовательно,
Представим константу C как lnC1, где C1 > 0. Тогда
Таким образом, заданное дифференциальное уравнение имеет следующие решения:
Полученный ответ можно упростить. В самом деле, введем произвольную константу C, принимающую значения от −∞ до +∞. Тогда решение можно записать в виде:
При C = 0, оно становится равным y = 0.
|
|
Пример 3
|
|
Найти все решения дифференциального уравнения y' = −xe y.
Решение.
Преобразуем уравнение следующим образом:
Очевидно, что деление на e y не приводит к потере решения, поскольку e y > 0. После интегрирования получаем
Данный ответ можно выразить в явном виде:
В последнем выражении предполагается, что константа C > 0, чтобы удовлетворить области определения логарифмической функции.
|
|
Пример 4
|
|
Найти частное решение дифференциального уравнения 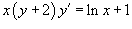 при условии y(1) = −1.
Решение.
Разделим обе части уравнения на x:
Мы предполагаем, что x ≠ 0, поскольку областью определения исходного уравнения является множество x > 0.
В результате интегрирования получаем:
Интеграл в правой части вычисляется следующим образом:
Следовательно, общее решение в неявной форме имеет вид:
где C1 = 2C − постоянная интегрирования.
Найдем теперь значение C1, удовлетворяющее начальному условию y(1) = −1:
Таким образом, частное решение дифференциального уравнения с заданным начальным условием (задача Коши) описывается алгебраическим уравнением:
|
|
Пример 5
|
|
Решить дифференциальное уравнение y' cot2 x + tan2 y = 0.
Решение.
Запишем данное уравнение в следующем виде:
Разделим обе части на tan y cot2 x:
Проверим, не потеряли ли мы какие-либо решения в результате деления. Необходимо исследовать следующие два корня:
Подставляя в исходное уравнение, мы видим, что 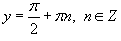 является решением уравнения.
Второе возможное решение описывается формулой
Здесь мы получаем ответ:
который не удовлетворяет исходному дифференциальному уравнению.
Теперь можно проинтегрировать дифференциальное уравнение и найти его общее решение:
Окончательный ответ записывается в виде:
|
|
Пример 6
|
|
Найти частное решение уравнения 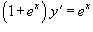 , удовлетворяющее начальному условию y(0) = 0.
Решение.
Перепишем уравнение в следующем виде:
Разделим обе части на 1 + ex:
Поскольку 1 + ex > 0, то при делении мы не потеряли никаких решений. Интегрируем полученное уравнение:
Теперь найдем константу C из начального условия y(0) = 0.
Следовательно, окончательный ответ имеет вид:
|
|
Пример 7
|
|
Решить уравнение 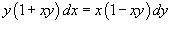 .
Решение.
Произведение xy в каждой части не позволяет разделить переменные. Поэтому, мы сделаем замену:
Соотношение для дифференциалов имеет вид:
Подставляя это в уравнение, получаем:
Далее, умножая обе части x, можно после соответствующих сокращений записать:
Учтем, что x = 0 является решением уравнения (это можно проверить непосредственной подстановкой).
Последнее выражение можно несколько упростить:
Теперь переменные x и t разделены:
В результате интегрирования находим:
Выполняя обратную подстановку t = xy, получаем общее решение дифференциального уравнения:
Полный ответ записывается в виде:
|
|
Пример 8
|
|
Найти общее решение дифференциального уравнения 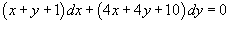 .
Решение.
Воспользуемся следующей подстановкой:
В результате уравнение принимает вид:
Следовательно,
Проинтегрируем последнее уравнение:
Поскольку u = x + y, то окончательный ответ в неявной форме записывается в виде:
|
|
|
|
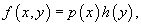
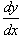 , перенесем dx в правую часть и разделим уравнение на
, перенесем dx в правую часть и разделим уравнение на 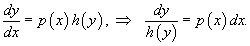
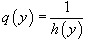 , запишем уравнение в форме:
, запишем уравнение в форме:
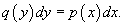
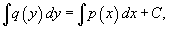
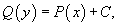
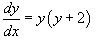 .
.
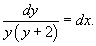
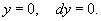
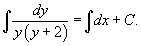
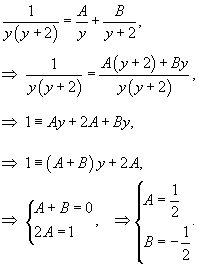
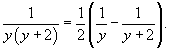
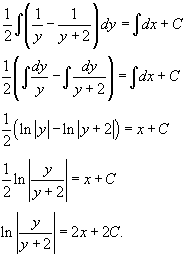
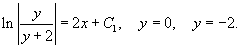
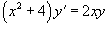 .
.
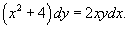
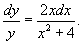
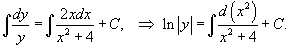
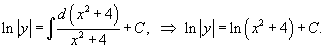
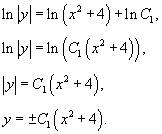
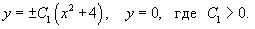

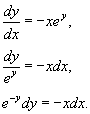
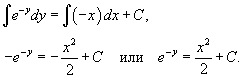
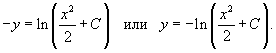
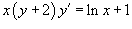 при условии
при условии 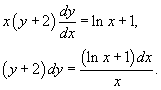
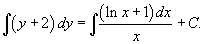
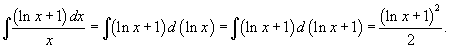
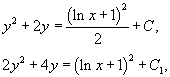
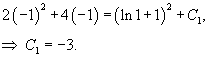
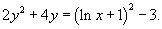
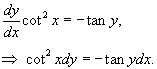
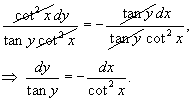
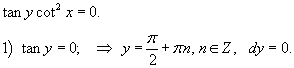
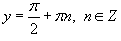 является решением уравнения.
является решением уравнения.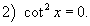
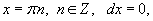
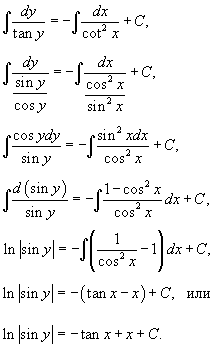
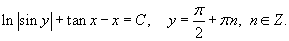
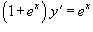 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 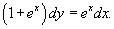
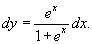
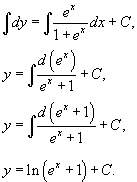
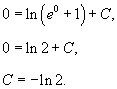
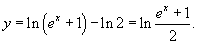
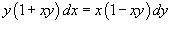 .
.
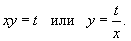
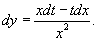
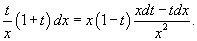
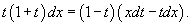
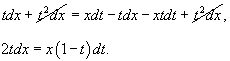
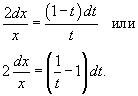
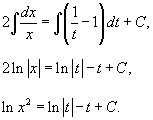
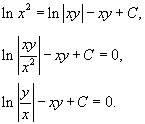
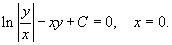
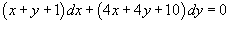 .
.