|
Линейные однородные системы дифференциальных уравнений с постоянными коэффициентами
|
|
Нормальная линейная система дифференциальных уравнений с постоянными коэффициентами n-го порядка записывается в виде
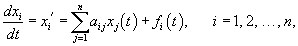 Будем считать, что все указанные функции являются непрерывными на некотором интервале Полагая 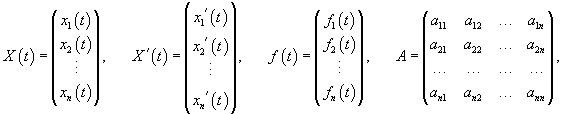 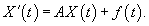 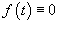 , то система называется однородной: , то система называется однородной:
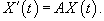
Метод исключения
Используя метод исключения, нормальную линейную систему n уравнений можно привести к одному линейному уравнению n-го порядка. Этот метод удобно использовать для решения простых систем − прежде всего, для систем 2-го порядка.Рассмотрим однородную систему двух уравнений с постоянными коэффициентами: 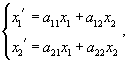 Продифференцируем первое уравнение и подставим производную 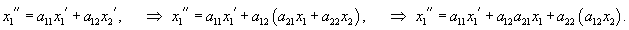 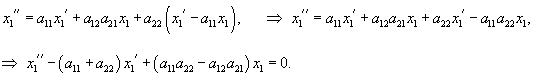 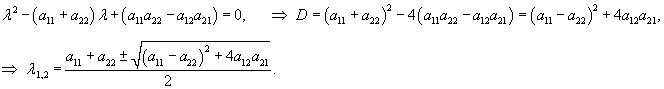 После определения функции Метод исключения можно применять не только к однородным линейным системам. Его можно использовать также для решения неоднородных систем дифференциальных уравнений или систем уравнений с переменными коэффициентами. |
|
Пример 1
|
|
Решить систему дифференциальных уравнений методом исключения:
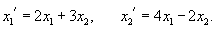
Решение.
Продифференцируем первое уравнение, затем подставим производную 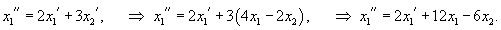 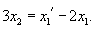 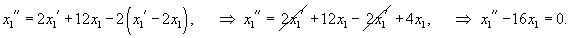 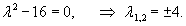  Теперь вычислим производную 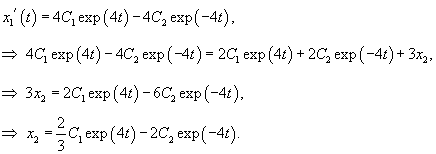 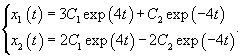 |
|
Пример 2
|
|
Решить систему уравнений методом исключения:

Решение.
Приведем данную систему к одному уравнению 2-го порядка для функции 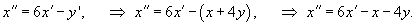 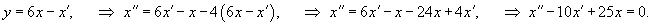 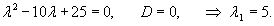 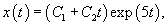 Найдем производную 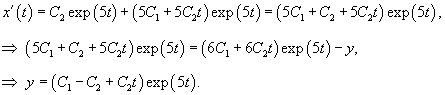 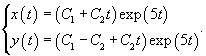 |
|
Пример 3
|
|
Найти общее решение системы уравнений
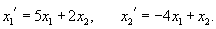
Решение.
Дифференцируя первое уравнение, получаем:
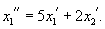 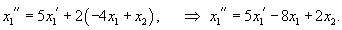 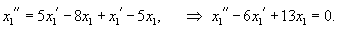 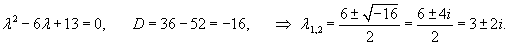 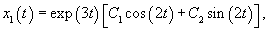 Найдем теперь другую функцию 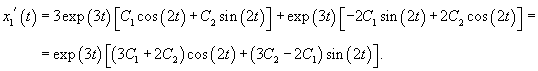 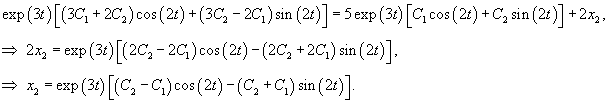 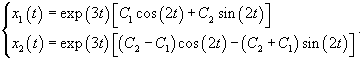 |