|
Метод собственных значений и собственных векторов
|
|
Понятие о собственных значениях и собственных векторах
Рассмотрим линейную однородную систему n дифференциальных уравнений с постоянными коэффициентами, которую можно записать в матричном виде как
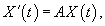 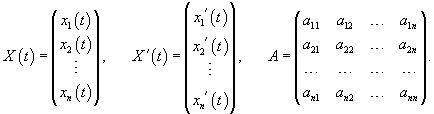 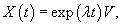 Подставляя указанное пробное выражение для 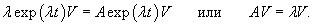 Таким образом, мы приходим к выводу, что для того, чтобы векторная функция Как видно, решение линейной системы уравнений можно построить алгебраическим методом. Поэтому приведем далее некоторые необходимые сведения из линейной алгебры.
Нахождение собственных значений и собственных векторов линейного преобразования
Вернемся к полученному выше матрично-векторному уравнению
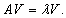 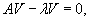 Вспомним, что произведение единичной матрицы I порядка n и n-мерного вектора V равно самому вектору: 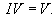 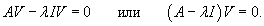 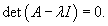 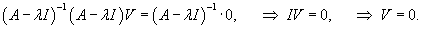 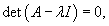 Итак, первый шаг в нахождении решения системы линейных дифференциальных уравнений − это решение характеристического уравнения и нахождение всех собственных значений Далее, подставляя каждое собственное значение λi в систему уравнений 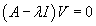
Фундаментальная система решений однородной линейной системы
Раскладывая определитель характеристического уравнения n-го порядка, мы получаем в общем случае следующее уравнение:
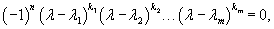 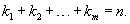 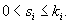
1. Случай В данном простейшем случае каждому собственному значению λi один собственный вектор Vi. Эти векторы образуют множество линейно независимых решений
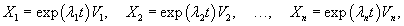 В силу линейной независимости собственных векторов соответствующий вронскиан будет отличен от нуля: 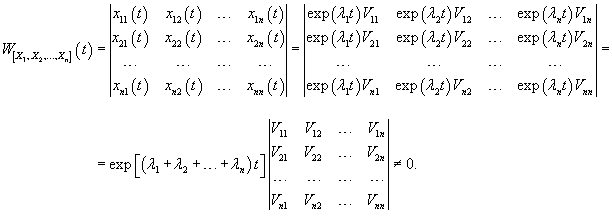 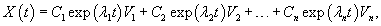 Характеристическое уравнение может иметь комплексные корни. Если при этом все коэффициенты матрицы A действительны, то комплексные корни появляются всегда в виде пар комплексно-сопряженных чисел. Предположим, что мы получили пару комплексных собственных значений 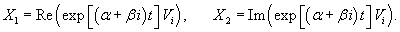
2. Случай Этот случай практически не отличается от предыдущего. Несмотря на наличие собственных значений с кратностью более 1, мы можем определить n линейно независимых собственных векторов. В частности, любая симметрическая матрица с действительными числами, у которой есть n собственных чисел, будет иметь n собственных векторов. Аналогичным свойством обладают унитарные матрицы. В общем случае квадратная матрица размером Общее решение системы n дифференциальных уравнений представляется в виде 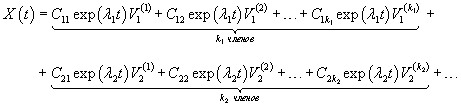
3. Случай В некоторых матрицах A (такие матрицы называются дефектными) собственное число λi кратностью ki может иметь меньше, чем ki линейно независимых собственных векторов. В этом случае вместо недостающих собственных векторов определяются так называемые присоединенные векторы, так чтобы в результате получить множество n линейно независимых векторов и построить соответствующую фундаментальную систему решений. Для этой цели обычно применяются два способа:
|
|
Пример 1
|
|
Найти общее решение системы дифференциальных уравнений
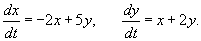
Решение.
Вычислим собственные значения λi матрицы A, составленной из коэффициентов заданных уравнений:
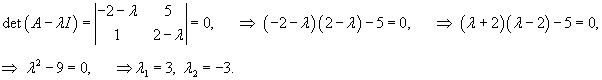 Найдем собственный вектор V1, соответствующий собственному числу 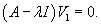 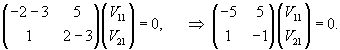 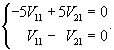 Аналогично определяем 2-ой собственный вектор V2, соответствующий  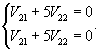 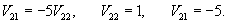 Таким образом, система уравнений имеет два различных собственных числа и два собственных вектора. Общее решение выражается формулой 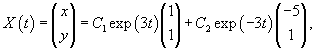 |
|
Пример 2
|
|
Найти общее решение системы дифференциальных уравнений
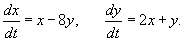
Решение.
Будем искать решение системы в виде
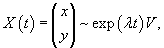 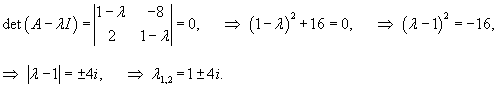 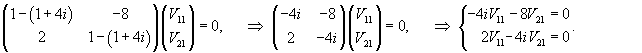 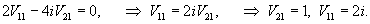 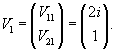 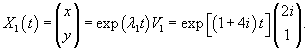 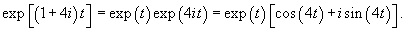 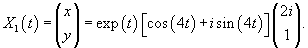 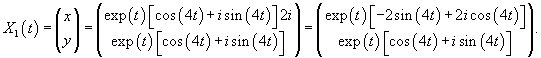 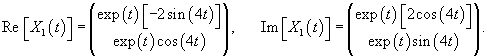 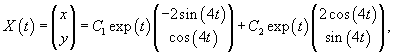 |
|
Пример 3
|
|
Найти общее решение системы дифференциальных уравнений
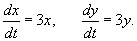
Решение.
Матрица данной системы имеет диагональный вид:
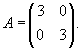  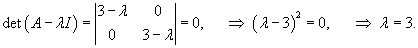 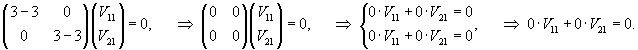 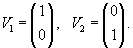 Общее решение системы уравнений записывается в виде 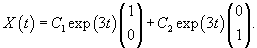 |
|
Пример 4
|
|
Найти общее решение системы дифференциальных уравнений
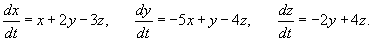
Решение.
Вычислим собственные значения матрицы A:
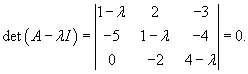 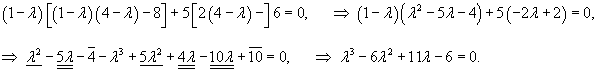 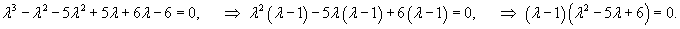 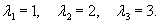 Найдем вектор V1 для числа 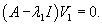 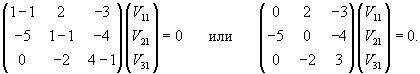 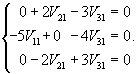 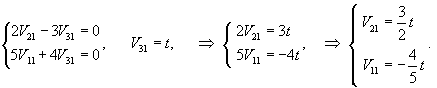 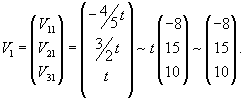 Аналогично найдем координаты второго собственного вектора V2, соответствующего числу 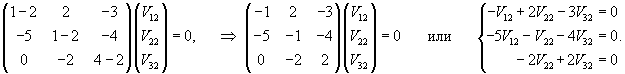 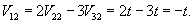 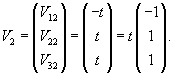 Вычислим теперь координаты третьего собственного вектора V3, соответствующего числу 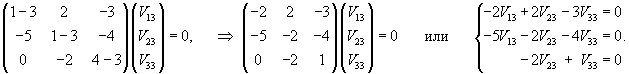 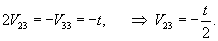 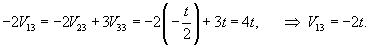 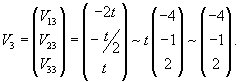 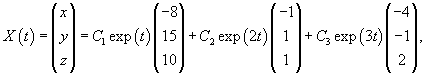 |
|
Пример 5
|
|
Найти общее решение системы уравнений
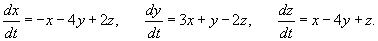
Решение.
Начнем с определения собственных значений матрицы A:
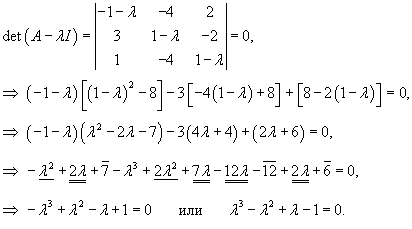 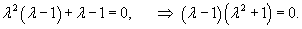  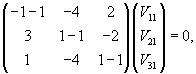 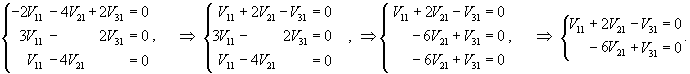 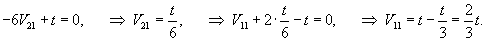 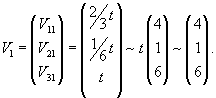 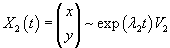 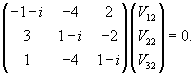 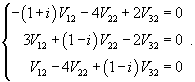  : :
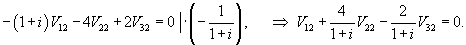 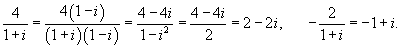 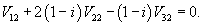 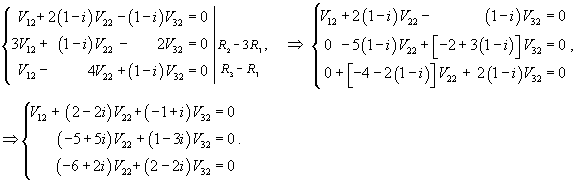 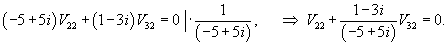 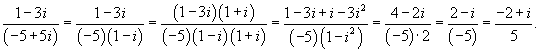 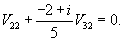 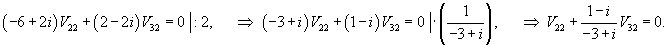 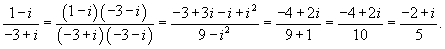 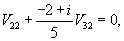 Итак, ранг системы равен 2 и ее можно записать в следующей эквивалентной форме: 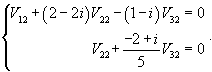 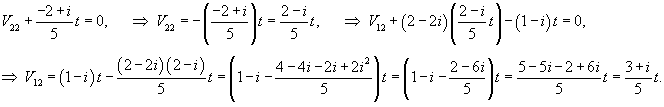 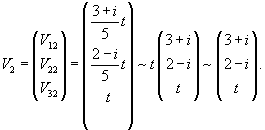 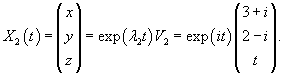 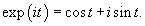 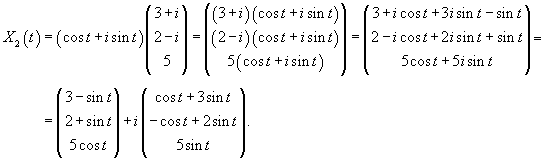 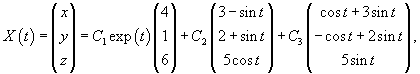 |
|
Пример 6
|
|
Найти общее решение системы дифференциальных уравнений
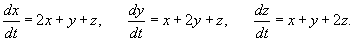
Решение.
Определим собственные значения заданной матрицы:
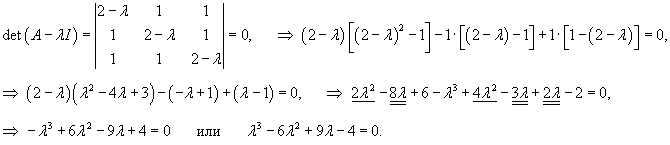 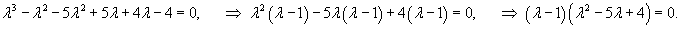 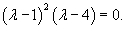 Определим собственные векторы, соответствующие числу 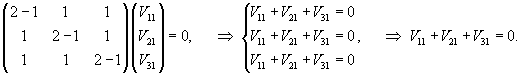 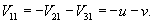 Соответственно, координаты второго линейно независимого собственного вектора (при Теперь определим третий собственный вектор V3, соответствующий числу 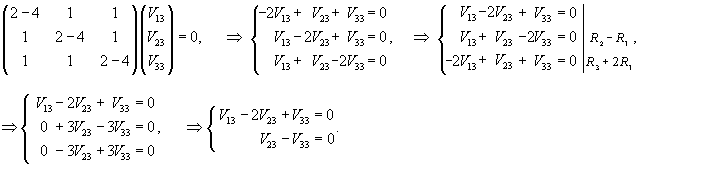 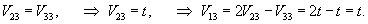 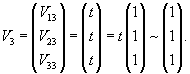 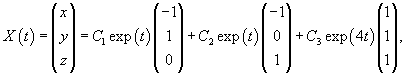 |