|
Построение общего решения системы уравнений с помощью жордановой формы
|
|
Снова рассмотрим линейную однородную систему n дифференциальных уравнений с постоянными коэффициентами:
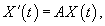 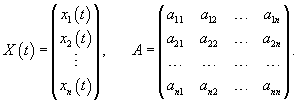 Рассмотрим эту технику решения более подробно. Предварительно введем некоторые базовые определения.
Жорданова форма матрицы
Жорданову форму можно рассматривать как обобщение квадратной диагональной матрицы. На ее диагонали размещаются т.н. жордановы клетки, соответствующие собственным значениям 
Присоединенные векторы и жордановы цепочки
Рассмотрим жорданову клетку размером k с собственным значением λ. Такой клетке соответствует k базисных векторов 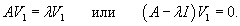 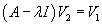 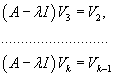 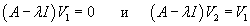 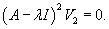 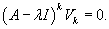 Каждой жордановой цепочке длины k соответствует k линейно-независимых решений однородной системы в виде 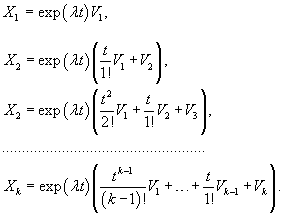
Общее решение системы для матриц 2x2 и 3x3
На практике наиболее часто встречаются системы дифференциальных уравнений 2-го и 3-го порядка. Рассмотрим все случаи жордановых форм, которые могут встретиться в таких системах, и соответствующие им формулы общего решения. Всего существует 8 различных случаев (3 для матрицы 2х2 и 5 для матрицы 3х3). Данную классификацию удобно проиллюстрировать следующей таблицей:
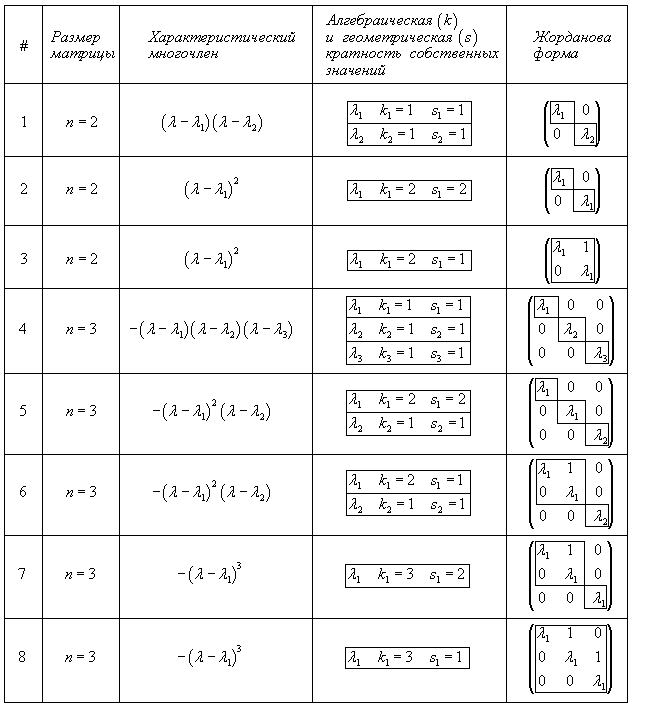
Случай 1. Матрица 2x2. Два различных собственных значения λ1, λ2
В этом случае жорданова форма имеет обычный диагональный вид. Каждому собственному значению λi соответствует один собственный вектор Vi, который находится из матричного уравнения
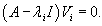 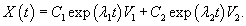
Случай 2. Матрица 2x2. Одно собственное значение Данная матрица имеет единственное собственное значение кратностью 2. Ранг матрицы при этом значении λ1 равен 1. Поэтому геометрическая кратность будет равна
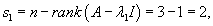 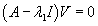 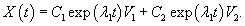
Случай 3. Матрица 2x2. Одно собственное значение Здесь ранг матрицы равен 2. Следовательно, геометрическая кратность собственного числа λ1 и количество собственных векторов равно
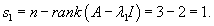 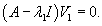 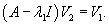 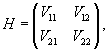 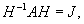 Общее решение системы представляется в виде: 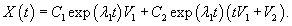
Случай 4. Матрица 3x3. Три различных собственных значения λ1, λ2, λ3
Здесь жорданова форма имеет диагональный вид. Каждому собственному числу λi соответствует свой собственный вектор Vi, который определяется из уравнения
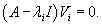 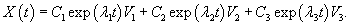
Случай 5. Матрица 3x3. Два собственных значения В данном случае характеристическое уравнение имеет два корня, один из которых кратный 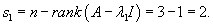 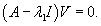 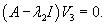 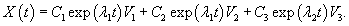
Случай 6. Матрица 3x3. Два собственных значения Этот случай отличается от предыдущего тем, что для первого собственного числа λ1 удается найти лишь один собственный вектор V1, который удовлетворяет уравнению
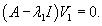 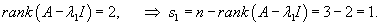 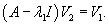 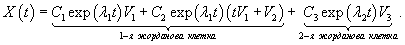
Случай 7. Матрица 3x3. Одно собственное значение Здесь жорданова форма состоит из двух клеток с одинаковым собственным значением λ1. Первая клетка имеет один собственный вектор V1 и один присоединенный вектор V2. Они находятся из соотношений
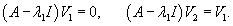 Общее решение системы описывается выражением 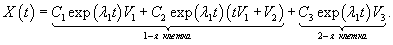
Случай 8. Матрица 3x3. Одно собственное значение В этом случае линейный оператор A имеет одно собственное значение λ1 кратностью 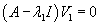  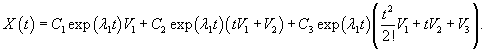 Ниже мы рассмотрим примеры систем уравнений, соответствующие случаям |
|
Пример 1
|
|
Решить систему уравнений
Решение.
Составим характеристическое уравнение для данной матрицы и найдем собственные значения:
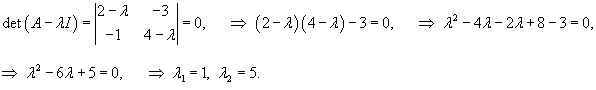 Подставляя 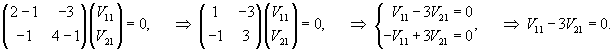 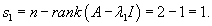 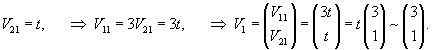 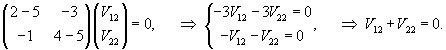 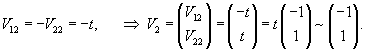 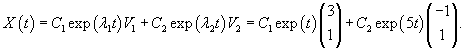 |
|
Пример 2
|
|
Найти общее решение системы уравнений
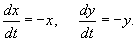
Решение.
Как обычно, определим сначала собственные значения, решив характеристическое уравнение
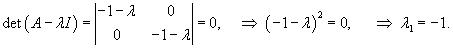 Найдем собственные векторы для этого значения λ1. 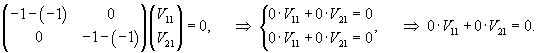 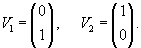 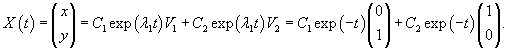 |
|
Пример 3
|
|
Найти общее решение системы уравнений
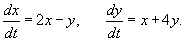
Решение.
Запишем характеристическое уравнение и найдем его корни:
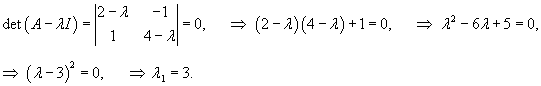 Определим собственные векторы, соответствующие числу 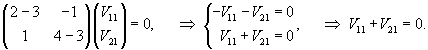 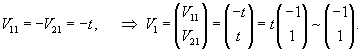 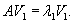 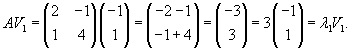 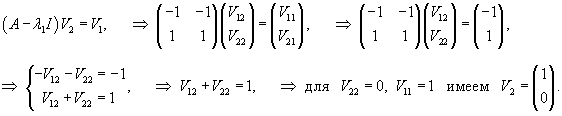 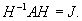 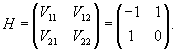 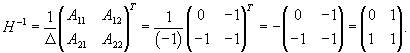 После подстановки убеждаемся, что результатом преобразований является жорданова форма: 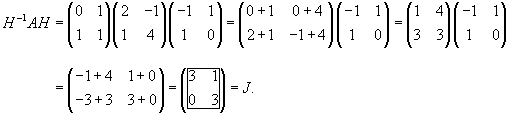 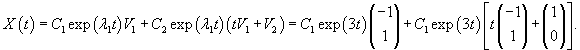 |
|
Пример 4
|
|
Решить систему уравнений
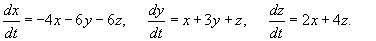
Решение.
Составим характеристическое уравнение и вычислим его корни:
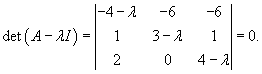 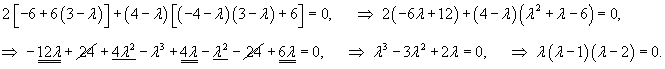 Вычислим собственные векторы V1, V2, V3 для этих собственных значений. Для собственного числа 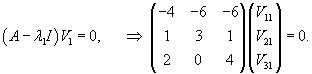 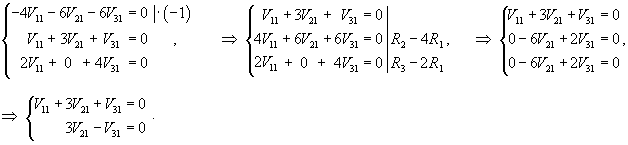 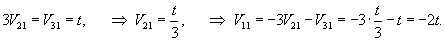 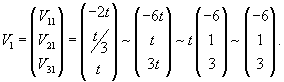 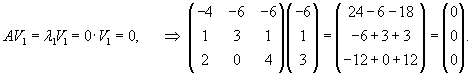 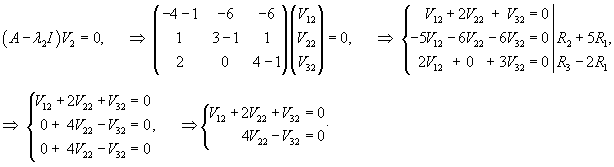 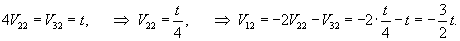 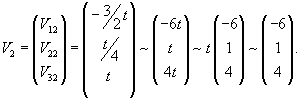 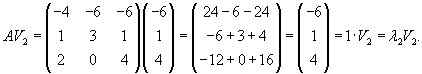 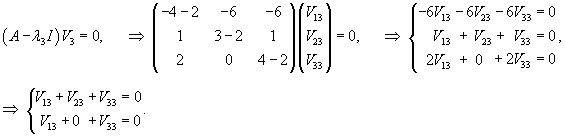 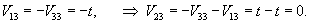 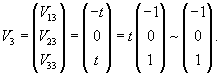 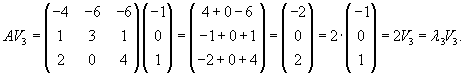 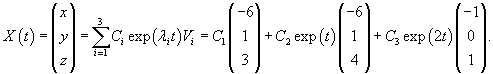 |
|
Пример 5
|
|
Найти общее решение системы дифференциальных уравнений
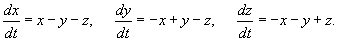
Решение.
Вычислим корни характеристического уравнения:
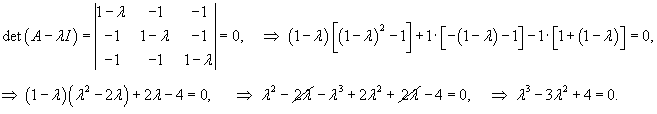 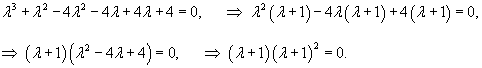 Определим собственные векторы. Для числа 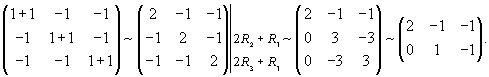  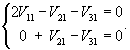 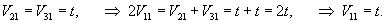 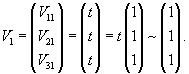 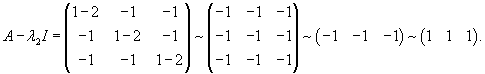 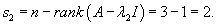 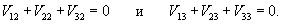 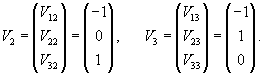 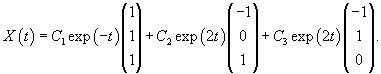 |
|
Пример 6
|
|
Найти общее решение системы уравнений
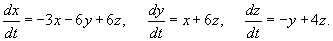
Решение.
Вычислим собственные значения:
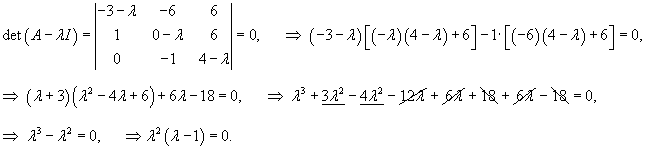 Вычислим ранг матрицы 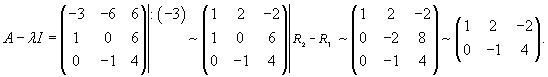 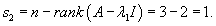 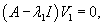 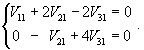 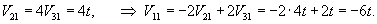 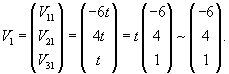 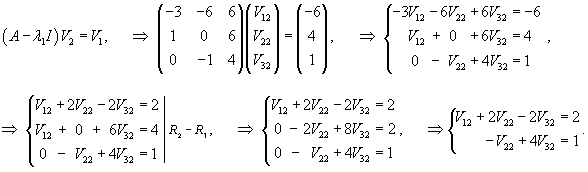 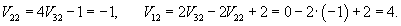 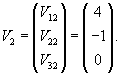 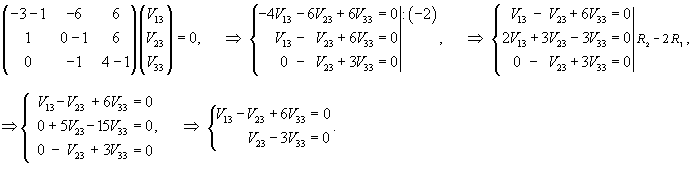 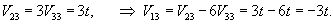 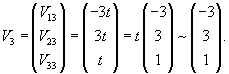 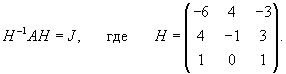 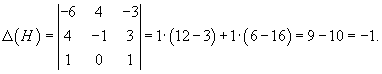 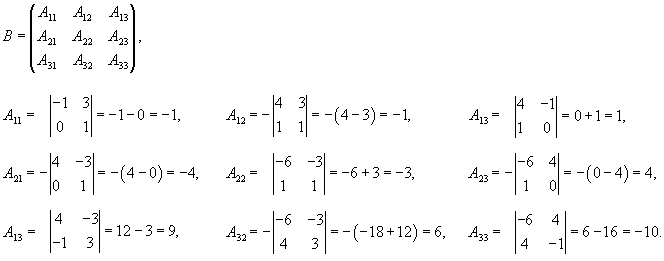 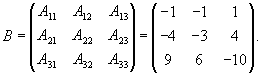 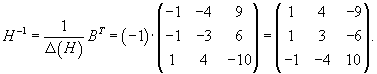 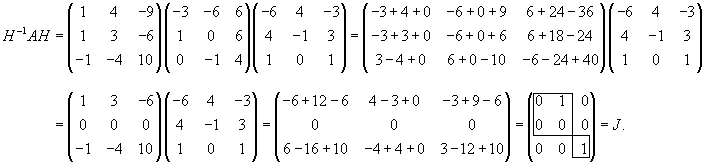 Общее решение системы выражается формулой 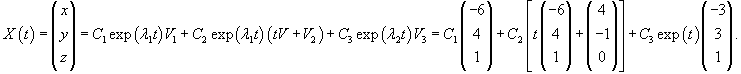 |
|
Пример 7
|
|
Найти общее решение системы линейных дифференциальных уравнений
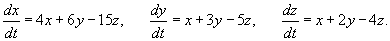
Решение.
Составим характеристическое уравнение и найдем собственные значения:
 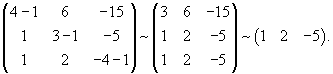 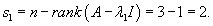 Найдем собственные векторы V1 и V2, ассоциированные с числом 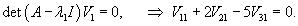 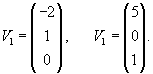 Рассмотрим жорданову клетку 2x2. Очевидно, что жорданова цепочка состоит из одного собственного вектора и одного присоединенного вектора. Обозначим эти векторы как U1 и U2. Они должны удовлетворять следующим матричным уравнениям: 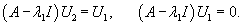 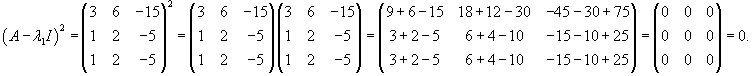 Вычислим вектор U1: 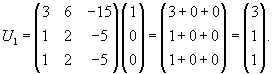 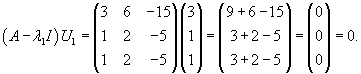 Вычисленные три линейно-независимых вектора U1, U2 и V2 образуют жорданов базис. Общее решение системы уравнений выражается в виде 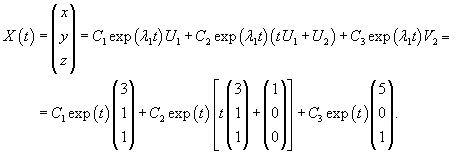 |
|
Пример 8
|
|
Решить систему линейных однородных уравнений
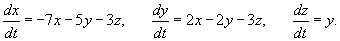
Решение.
Составляем характеристическое уравнение и находим его корни:
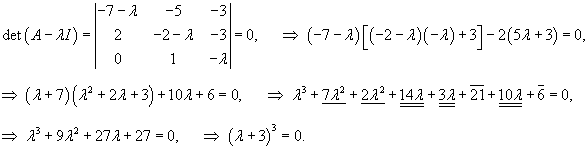 Вычислим ранг матрицы 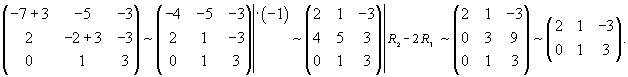 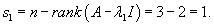 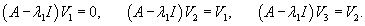 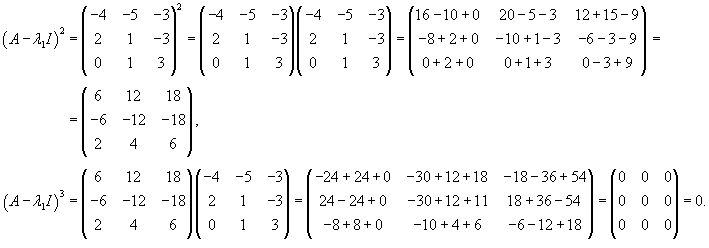 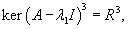 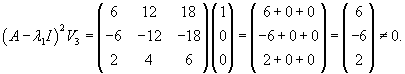 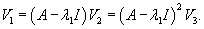 Продолжая вычисления, находим V2 и V1: 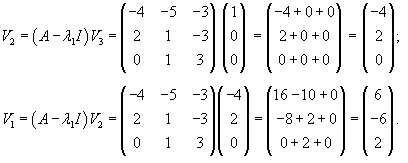 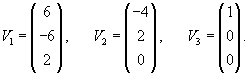 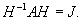 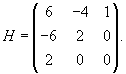 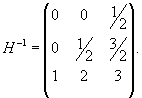 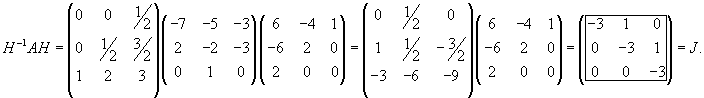 Общее решение системы имеет вид: 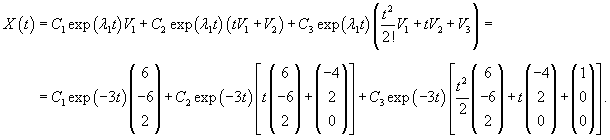 |