|
Дифференциалы высшего порядка
|
|
Определение дифференциала высшего порядка
Рассмотрим функцию y = f(x), которая является дифференцируемой на интервале (a, b). Дифференциал первого порядка данной функции в точке x ∈ (a, b) определяется формулой
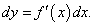 Зафиксируем приращение dx, т.е. будем считать, что dx является постоянной величиной. Тогда дифференциал dy представляет собой функцию только переменной x, для которой можно также определить дифференциал, причем в качестве приращения Δx возьмем тот же самый дифференциал dx. В результате мы получим второй дифференциал или дифференциал второго порядка, который обозначается как d 2y или d 2f(x). Итак, по определению, 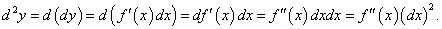 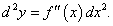 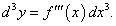 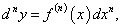 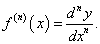 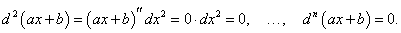 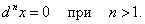
Свойства дифференциала n-го порядка
Пусть функции u и v имеют производные n-го порядка. Тогда справедливы следующие свойства:
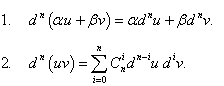
Дифференциал n-го порядка сложной функции
Рассмотрим теперь композицию двух функций, таких, что y = f(u) и u = g(x). В таком случае y является сложной функцией от независимой переменной x:
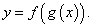  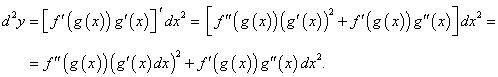 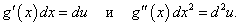 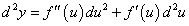 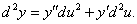 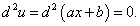 |
|
Пример 1
|
|
Найти дифференциал d 4y для функции y = x5.
Решение. 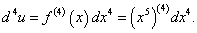 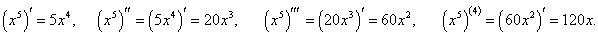 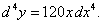 |
|
Пример 2
|
|
Дана функция
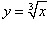 . Найти d 2y. . Найти d 2y.
Решение. 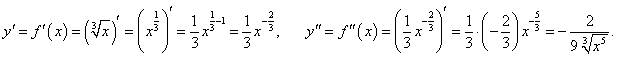 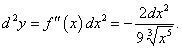 |
|
Пример 3
|
|
Найти второй дифференциал функции y = x2cos 2x.
Решение.  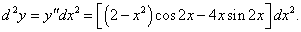 |
|
Пример 4
|
|
Найти дифференциал 4-го порядка функции y = √2x + 1.
Решение. 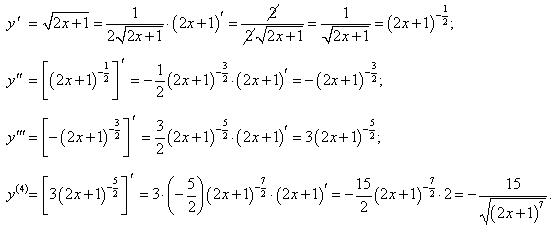 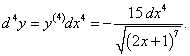 |
|
Пример 5
|
|
Найти d 3y для функции y = x2 ln x.
Решение. 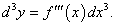 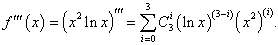  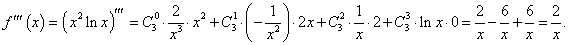 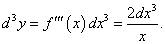 |
|
Пример 6
|
|
Дана функция
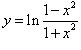 . Найти d 2y. . Найти d 2y.
Решение. 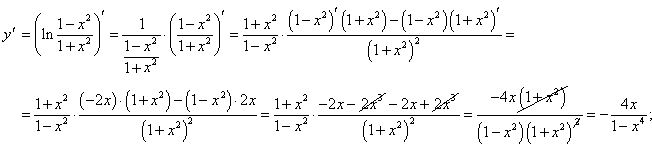 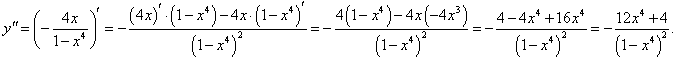 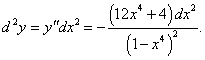 |
|
Пример 7
|
|
Найти дифференциал 5-го порядка функции y = x cos x.
Решение. 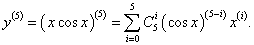 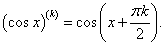 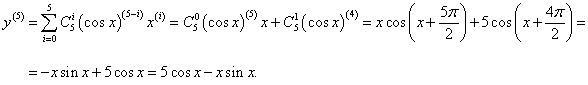 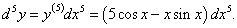 |
|
Пример 8
|
|
Найти дифференциал d 8y для функции y = e xsin x.
Решение. 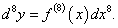 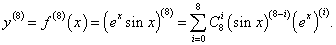 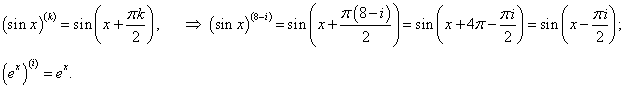  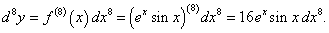 |
|
Пример 9
|
|
Дана функция y = sin x ch x. Найти d 3y.
Решение. 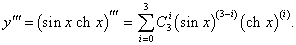 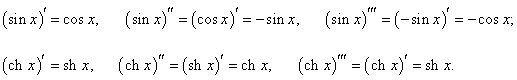 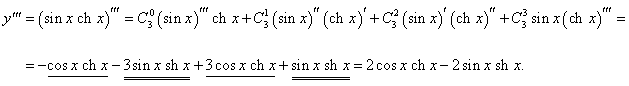 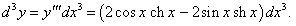 |
|
Пример 10
|
|
Найти второй дифференциал d 2y астроиды, заданной уравнением x2/3 + y2/3 = R2/3.
Решение. 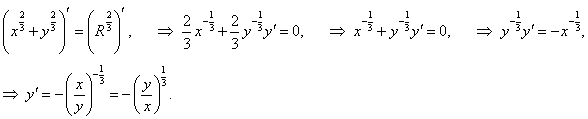 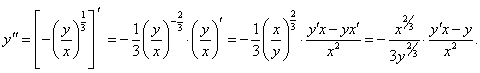 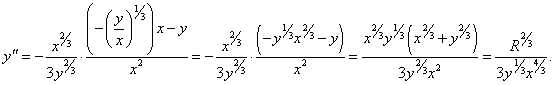 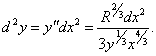 |
|
Пример 11
|
|
Функция задана в параметрической форме уравнениями
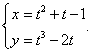 Решение. 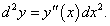 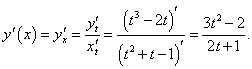 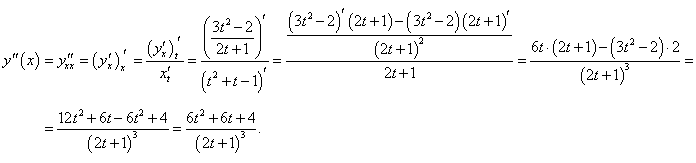 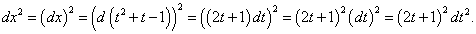 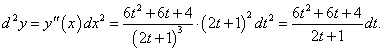 |
|
Пример 12
|
|
Уравнение верхней полуокружности с центром в начале координат и радиусом R в параметрической форме имеет вид
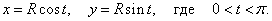 Решение. 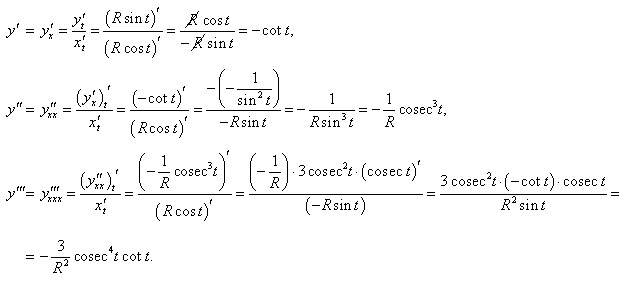 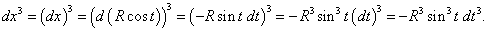 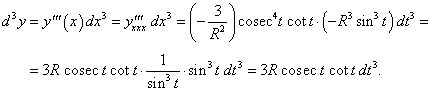 |