|
Дифференциал функции
|
||||||
|
Определение дифференциала
Рассмотрим функцию y = f(x), которая является непрерывной в интервале [a, b]. Предположим, что в некоторой точке x0∈ [a, b] независимая переменная получает приращение Δx. Приращение функции Δy, соответствующее такому изменению аргумента Δx, выражается формулой
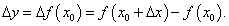 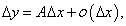
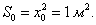 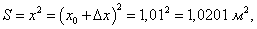 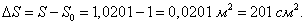  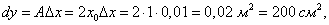 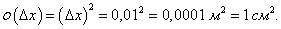 Заметим, что в данном примере коэффициент A равен значению производной функции S в точке x0: 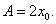 Коэффициент A главной части приращения функции в точке x0 равен значению производной f'(x0) в этой точке, т.е. приращение Δy выражается формулой 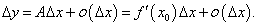 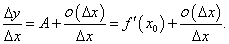 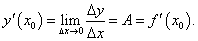 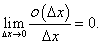 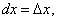 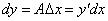 
Геометрический смысл дифференциала функции
На рисунке 2 схематически показана разбивка приращения функции Δy на главную часть AΔx (дифференциал функции) и член высшего порядка малости o(Δx).Касательная MN, проведенная к кривой функции y = f(x) в точке M, как известно, имеет угол наклона α, тангенс которого равен производной: 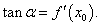
Свойства дифференциала
Пусть u и v − функции переменной x. Дифференциал обладает следующими свойствами:
Как видно, дифференциал функции dy отличается от производной лишь множителем dx. Например, 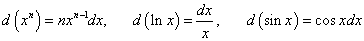
Инвариантность формы дифференциала
Рассмотрим композицию двух функций y = f(u) и u = g(x), т.е. сложную функцию y = f(g(x)). Ее производная определяется выражением
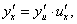 Дифференциал "внешней" функции y = f(u) записывается в виде  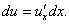 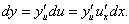 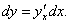 |
||||||
|
Пример 1
|
||||||
|
Найти дифференциал функции y = sin x − x cos x.
Решение. 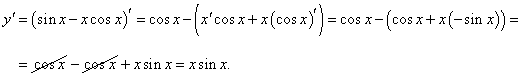 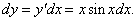 |
||||||
|
Пример 2
|
||||||
|
Найти дифференциал функции
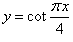 в точке x = 1. в точке x = 1.
Решение. 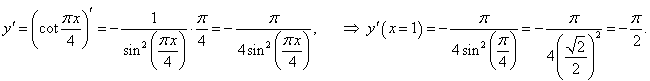 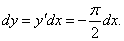 |
||||||
|
Пример 3
|
||||||
|
Найти дифференциал функции y = 2x2 + 3x + 1 в точке x = 1 при dx = 0.1
Решение. 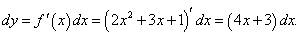 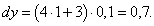 |
||||||
|
Пример 4
|
||||||
|
Вычислить приращение и дифференциал функции y = x2 − x + 1 в точке x = 2 при Δx = 1.
Решение. 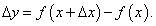 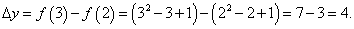 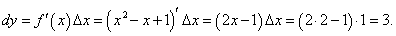 |
||||||
|
Пример 5
|
||||||
|
Найти дифференциал функции y = xxe2x в точке x = 1.
Решение. 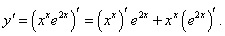 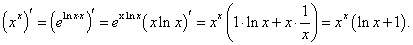 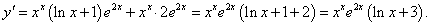 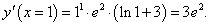 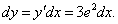 |
||||||
|
Пример 6
|
||||||
|
Найти дифференциал функции
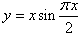 в точке x = 1/2 при dx = 0,01. в точке x = 1/2 при dx = 0,01.
Решение. 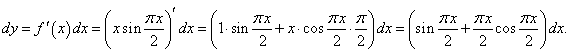  |
||||||
|
Пример 7
|
||||||
|
Вычислить приращение и дифференциал функции
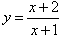 в точке x = 0 при Δx = 0,1. в точке x = 0 при Δx = 0,1.
Решение. 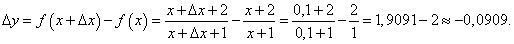 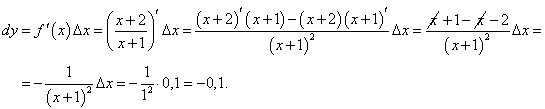 |
||||||
|
Пример 8
|
||||||
|
Найти дифференциал функции
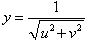 , где u и v − дифференцируемые функции переменной x. , где u и v − дифференцируемые функции переменной x.
Решение. 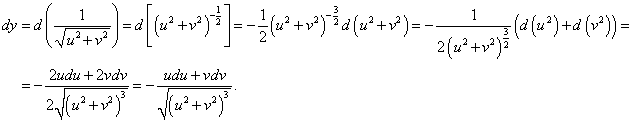 |
||||||
|
Пример 9
|
||||||
|
Найти дифференциал функции
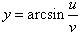 , где u и v − дифференцируемые функции от x. , где u и v − дифференцируемые функции от x.
Решение. 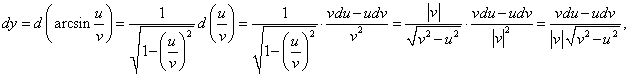 |
||||||
|
Пример 10
|
||||||
|
Функция y(x) задана неявным уравнением y3 − 3xy + x3 = 3. Найти ее дифференциал в точке (2, 1).
Решение. 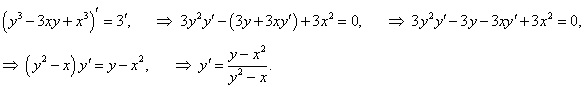 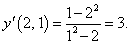 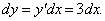 |
||||||
|
Пример 11
|
||||||
|
Функция y(x) задана неявным уравнением x2 − √y ln y = 1. Найти ее дифференциал в точке (1, 1).
Решение. 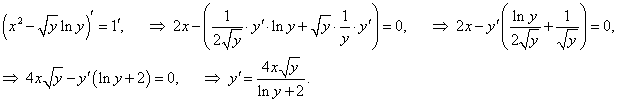 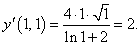 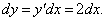 |
||||||
|
Пример 12
|
||||||
|
Найти дифференциал функции
 . .
Решение. 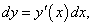 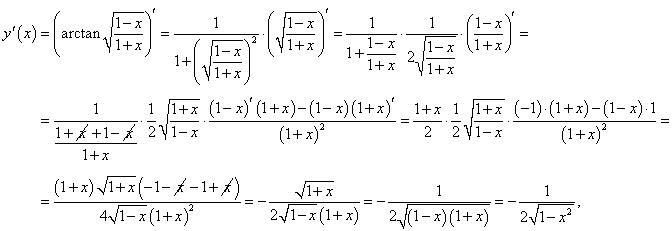 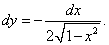 |
||||||
|
Пример 13
|
||||||
|
Функция y(x) задана параметрическими уравнениями
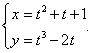 Решение. 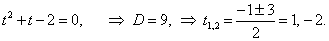 Найдем производную y'x параметрически заданной функции: 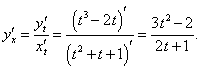 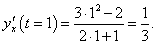 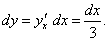 |
||||||
|
Пример 14
|
||||||
|
Функция y(x) задана параметрическими уравнениями
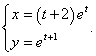 Решение. 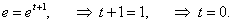 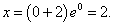 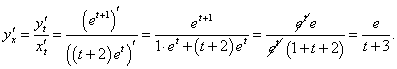 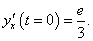 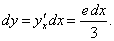 |
||||||
|
Пример 15
|
||||||
|
Дана сложная функция y = ln u, u = cos x. Выразить дифференциал функции y в инвариантной форме.
Решение. 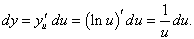 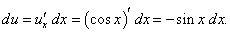 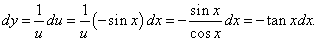 |
||||||