|
Формула Лейбница
|
|
Формула Лейбница выражает производную n-го порядка от произведения двух функций. Пусть функции u(x) и v(x) имеют производные до n-го порядка включительно. Рассмотрим производные от произведения данных функций.
Первая производная описывается известной формулой 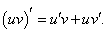 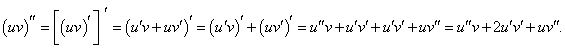 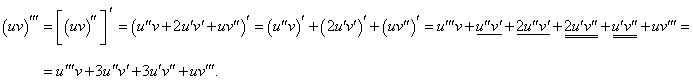 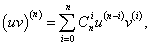 Приведенная формула называется формулой Лейбница и доказывается методом математической индукции. Доказательство. Предположим, что для функций u и v существуют также производные (n + 1)-го порядка. Используя рекуррентное соотношение, запишем выражение для производной (n + 1)-го порядка в следующем виде: 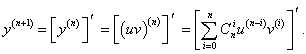 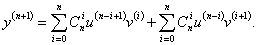 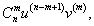 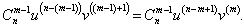 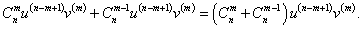 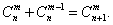 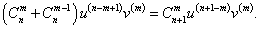 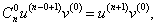 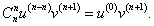 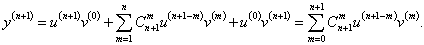 |
|
Пример 1
|
|
Найти третью производную функции y = e2x ln x.
Решение. 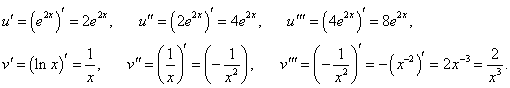 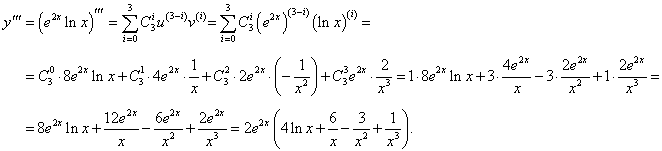 |
|
Пример 2
|
|
Найти все производные функции y = exx2.
Решение. 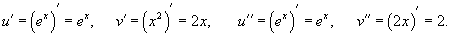 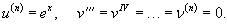  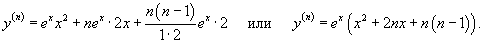 |
|
Пример 3
|
|
Дана функция y = x2cos 3x . Найти производную третьего порядка.
Решение. 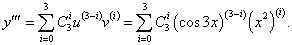 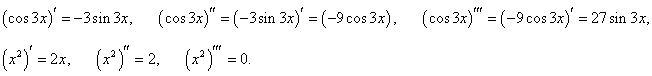 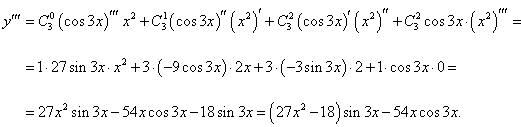 |
|
Пример 4
|
|
Найти производную 5-го порядка функции y = (x3 + 2x2 + 3x)ex.
Решение. 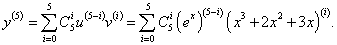 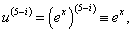 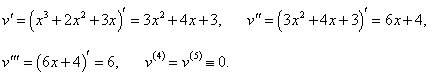 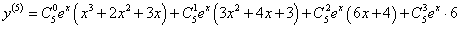 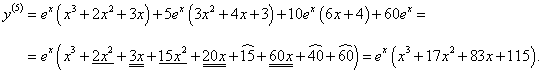 |
|
Пример 5
|
|
Найти производную n-го порядка функции y = x2cos x.
Решение. 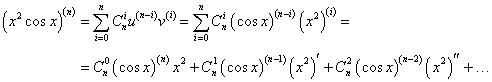 На странице Производные высшего порядка в примере 7 была определена производная n-го порядка функции косинус: 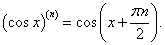 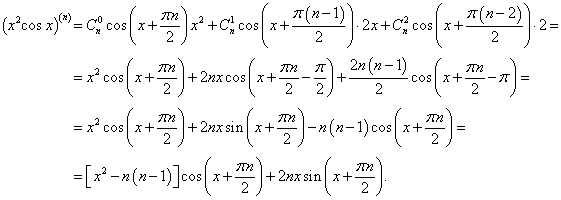 |
|
Пример 6
|
|
Найти производную 10-го порядка функции
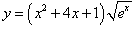 в точке x = 0. в точке x = 0.
Решение. 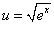 , v = x2 + 4x + 1. Производные этих функций имеют такой вид: , v = x2 + 4x + 1. Производные этих функций имеют такой вид:
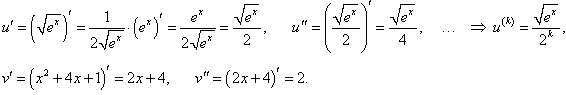 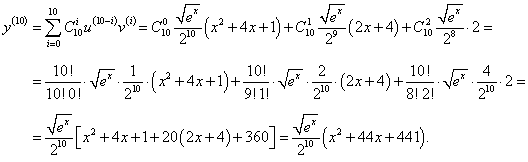 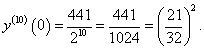 |
|
Пример 7
|
|
Найти производную n-го порядка функции y = x3sin 2x.
Решение. 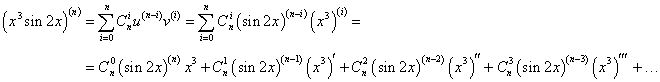 В примере 6 на странице Производные высшего порядка была найдена производная n-го порядка функции синус: 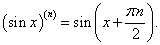 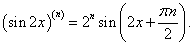 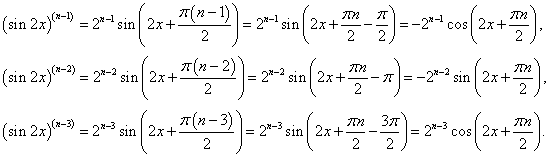 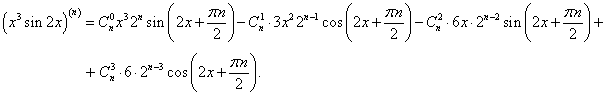 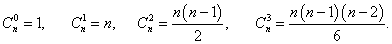 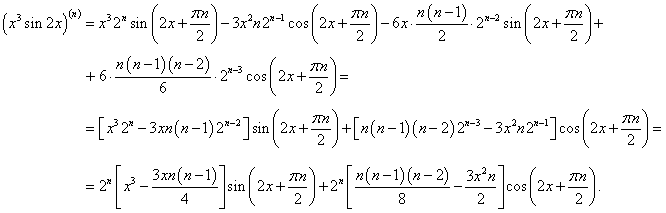 |
|
Пример 8
|
|
Найти производную n-го порядка функции y = (3x2 − 2x) ln x, x > 0.
Решение. 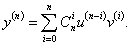 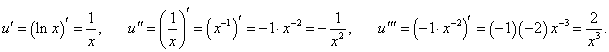 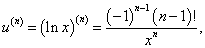 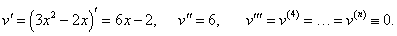 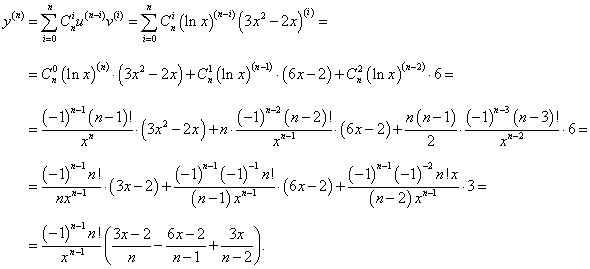 |
|
Пример 9
|
|
Найти производную 4-го порядка функции y = (x3 − x2) tan x в точке x = 1.
Решение. 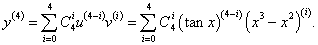 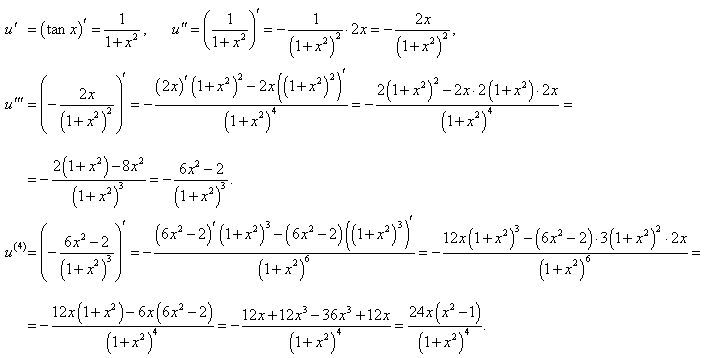 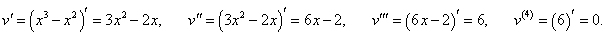 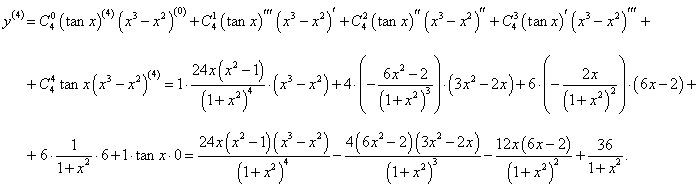 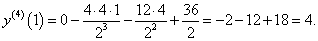 |
|
Пример 10
|
|
Найти производную n-го порядка функции y = arctan x в точке x = 0.
Решение. 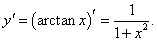 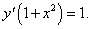  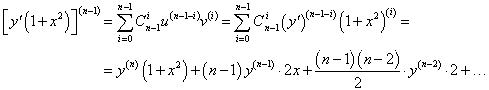 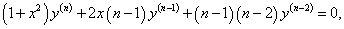 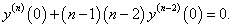 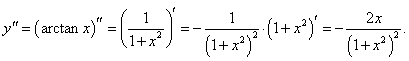 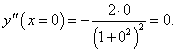 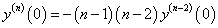 Для нечетных n (n = 2k + 1, k = 0, 1, 2, ...) рекуррентную формулу можно записать в таком виде: 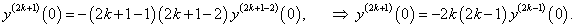 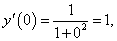 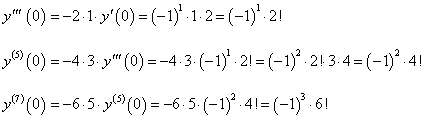 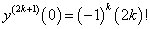 |