Локальные экстремумы функции

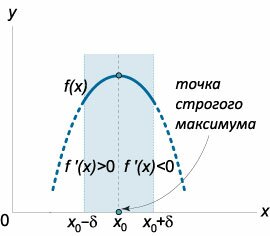
Пусть функция y = f(x) определена в некоторой δ-окрестности точки x₀, где δ > 0. Говорят, что функция f(x) имеет локальный максимум в точке x₀, если для всех точек x ≠ x₀, принадлежащих окрестности  (x₀− δ, x₀ + δ)  выполняется неравенство Если для всех точек x ≠ x₀ из некоторой окрестности точки x₀ выполняется строгое неравенство то точка x₀ является точкой строгого локального максимума.

Аналогично определяется локальный минимум функции f(x). В этом случае для всех точек x ≠ x₀ из δ-окрестности  (x₀− δ, x₀ + δ)  точки x₀ справедливо неравенство Соответственно, строгий локальный минимум описывается строгим неравенством Понятия локального максимума и локального минимума объединяются общим термином локальный экстремум. Слово "локальный" для краткости часто опускают и говорят просто о максимумах и минимумах функции. На рисунке 1 схематически показаны различные точки экстремума. Точка A(x₁) является точкой строгого локального минимума, поскольку для нее существует δ-окрестность  (x₀− δ, x₀ + δ),  в которой справедливо неравенство Аналогично, точка B(x₂) является точкой строгого локального максимума. В этой точке выполняется неравенство (Разумеется, число δ в каждой точке может быть совершенно разным.)

Последующие точки классифицируются таким образом:

• точка C(x₃) − строгий минимум;


• точка D(x₄) − нестрогий максимум;


• точка E(x₅) − нестрогий максимум или минимум;


• точка F(x₆) − нестрогий максимум;


• точка G(x₇) − нестрогий минимум;


• точка H(x₈) − нестрогий максимум или минимум;


• точка I(x₉) − нестрогий максимум;


• точка J(x₁₀) − экстремума нет.

Введем еще некоторые понятия.

Точки, в которых производная функции f(x) равна нулю, называются стационарными точками.

Точки, в которых производная функции f(x) равна нулю либо не существует, называются критическими точками данной функции. Следовательно, стационарные точки являются подмножеством множества критических точек.

Необходимое условие экстремума формулируется следующим образом:

Если точка x₀ является точкой экстремума функции f(x), то в этой точке либо производная равна нулю, либо не существует. Другими словами, экстремумы функции содержатся среди ее критических точек.

Доказательство необходимого условия экстремума следует из теоремы Ферма.

Отметим, что выполнение необходимого условия еще не гарантирует существование экстремума. Классической иллюстрацией здесь является кубическая функция  f(x) = x³. Несмотря на то, что в точке x = 0 производная данной функции равна нулю:  f ' (x = 0) = 0,  эта точка не является экстремумом.

Экстремумы дифференцируемых функций существуют при выполнении достаточных условий. Эти условия основаны на использовании производной первого, второго или высшего порядка. Соответственно, рассматриваются 3 достаточных условия экстремума. Перейдем к их формулировке и доказательству. Пусть функция f(x) дифференцируема в некоторой окрестности точки x₀, кроме, быть может, самой точки x₀, в которой, однако, функция непрерывна. Тогда:

• Если производная f '(x) меняет знак с минуса на плюс при переходе через точку x₀ (слева направо), то точка x₀ является точкой строгого минимума (рис.2). Другими словами, в этом случае существует число δ > 0, такое, что
  ∀ x ∈ (x₀ − δ, x₀)   ⇒   f '(x) < 0,
  ∀ x ∈ (x₀, x₀ + δ)   ⇒   f '(x) > 0.
• Если производная f '(x), наоборот, меняет знак с плюса на минус при переходе через точку x₀, то точка x₀ является точкой строгого максимума (рис.3). Иначе говоря, существует число δ > 0, такое, что
  ∀ x ∈ (x₀ − δ, x₀)   ⇒   f '(x) > 0,
  ∀ x ∈ (x₀, x₀ + δ)   ⇒   f '(x) < 0.

Доказательство.
Ограничимся рассмотрением случая минимума. Пусть производная f '(x) при переходе через точку x₀ меняет знак с минуса на плюс. Слева от точки x₀ выполняется условие По теореме Лагранжа разность значений функции в точках x и x₀ записывается как где точка c принадлежит интервалу (x₀ − δ, x₀), в котором производная отрицательна, т.е. f '(c) < 0. Поскольку x − x₀ < 0 слева от точки x₀, то следовательно, Таким же образом устанавливается, что (справа от точки x₀).

На основании определения заключаем, что точка x₀ является точкой строгого минимума функции f(x).

Аналогично можно доказать первое достаточное условие для строгого максимума функции.

Заметим, что в первом достаточном условии не требуется, чтобы функция была дифференцируемой в точке x₀. Если в этой точке производная равна бесконечности или не существует (т.е. точка x₀ является критической, но не стационарной), то первое достаточное условие все равно можно использовать для исследования функции на максимум или минимум. Пусть в точке x₀ первая производная равна нулю:  f(x₀) = 0,  т.е. точка x₀ является стационарной точкой функции f(x). Пусть также в этой точке существует вторая производная  f ''(x₀). Тогда:

• Если  f ''(x₀) > 0, то x₀ является точкой строгого минимума функции f(x);
• Если  f ''(x₀) < 0, то x₀ является точкой строгого максимума функции f(x).

Доказательство.
В случае строгого минимума  f ''(x₀) > 0. Тогда первая производная представляет собой возрастающую функцию в точке x₀. Следовательно, найдется число δ > 0, такое, что Поскольку  f '(x₀) = 0 (так как x₀ − стационарная точка), то следовательно, в δ-окрестности слева от точки x₀ первая производная отрицательна, а справа − положительна, т.е. первая производная меняет знак с минуса на плюс при переходе через точку x₀. По первому достаточному признаку экстремума это означает, что x₀ − точка строгого минимума.

Аналогично рассматривается случай максимума.

Второй достаточный признак экстремума удобно применять, когда вычисление первых производных в окрестности стационарной точки затруднительно. С другой стороны, второй признак можно использовать лишь для стационарных точек (где первая производная равна нулю) − в отличие от первого признака, который применим к любым критическим точкам. Пусть функция f(x) имеет в точке x₀ производные до n-го порядка включительно. Тогда, если то при четном n точка x₀ является

• − точкой строгого минимума, если  f ⁿ(x₀) > 0, и
• − точкой строгого максимума, если  f ⁿ(x₀) < 0.

При нечетном n экстремума в точке x₀ не существует.

Ясно, что при n = 2 в качестве частного случая мы получаем рассмотренное выше второе достаточное условие экстремума. Чтобы исключить такой переход, в третьем признаке полагают, что n > 2.

Доказательство.
Разложим функцию f(x) в точке x₀ в ряд Тейлора: Поскольку по условию теоремы все первые производные до (n − 1)-го порядка равны нулю, получаем: где остаточный член  ο((x − x₀) ⁿ) имеет более высокий порядок малости, чем n. В результате в δ-окрестности точки x₀ знак разности  f((x) − f(x₀)  будет определяться знаком n-го члена в ряде Тейлора: или Если n − четное число (n = 2k), то Следовательно, в этом случае При  f ⁽ⁿ⁾(x₀) > 0 в δ-окрестности точки x₀ выполняется неравенство По определению это означает, что x₀ − точка строгого минимума функции f(x).

Аналогично, при  f ⁽ⁿ⁾(x₀) < 0 в δ-окрестности точки x₀ имеем неравенство что соответствует точке строгого максимума.

Если n − нечетное число (n = 2k + 1), то степень (x − x₀)^2k+1 будет менять знак при переходе через точку x₀. Тогда из формулы следует, что разность  f((x) − f(x₀)  также меняет знак при переходе через x₀. В этом случае экстремума в точке x₀ не существует.

   Пример 1

Найти экстремумы функции  f(x) = − x² + 4x − 3. Данная функция дифференцируема всюду на множестве ℜ. Следовательно, экстремумы функции содержатся среди ее стационарных точек. Решаем уравнение f '(x) = 0: Функция имеет одну стационарную точку x = 2. Определим знаки производной слева и справа от точки x = 2. При x < 2 производная положительна, а при x > 2 − отрицательна. Таким образом, при переходе через точку x = 2 производная меняет знак с плюса на минус. По первому достаточному признаку экстремума это означает, что x = 2 является точкой максимума.

Сам максимум (т.е. значение функции в точке максимума) равен:

   Пример 2

Найти экстремумы кубической функции  f(x) = x³ − 3x² − 9x + 2. Функция дифференцируема на всем множестве действительных чисел. Поэтому экстремумы содержатся среди стационарных точек, где производная равна нулю. Находим эти точки: Подставляя пробные значения x, определяем знаки производной  f '(x) = 3x² − 6x - 9  в соответствующих интервалах (рисунок 4).

Как видно, при переходе через точку x = −1 производная меняет знак с плюса на минус. По первому достаточному признаку экстремума эта точка является точкой максимума. Аналогично устанавливаем, что x = 2 − точка минимума.

Определим теперь сами экстремумы, т.е. вычислим значение функции в точках максимума и минимума:

   Пример 3

Найти экстремумы функции  f(x) = x^1/x. Данная функция относится к семейству показательно-степенных функций. В общем случае они имеют вид  y = g(x)^h(x).  Обычно считают, что область определения показательно-степенных функций удовлетворяет условию g(x) > 0. (В некоторых частных случаях основание g(x) может быть отрицательным − например, если h(x) = 1/3.) В нашем случае полагаем x > 0. Отсюда следует, что функция принимает лишь положительные значения.

Вычисляем производную: Примечание: Производную функции  f(x) = x^1/x можно найти также с помощью логарифмического дифференцирования.

Определяем критические точки: В левой окрестности точки  x = e  производная положительна, а в правой окрестности − отрицательна. Следовательно, в точке  x = e  функция достигает максимума, равного

   Пример 4

Найти экстремумы функции  f(x) = x²e^{− x}. Функция определена и дифференцируема на всем множестве ℜ. Вычислим ее производную: Найдем корни уравнения f '(x) = 0: При переходе через найденные точки производная меняет знак так, как показано выше на рисунке 5. Следовательно, в точке x = 0 функция имеет минимум, а в точке x = 0 − максимум. Значения минимума и максимума, соответственно, составляют:

   Пример 5

Найти экстремумы функции  f(x) = x + cos2x. Функция дифференцируема на всем множестве ℜ. Вычислим производную и определим стационарные точки: Полученное тригонометрическое уравнение имеет две ветви решений: Чтобы определить тип экстремума, воспользуемся вторым достаточным признаком. Найдем вторую производную: Для первого множества решений (2x = π/6 +2πn,  n ∈ Z) вторая производная отрицательна. Следовательно, это множество соответствует точкам максимума. Второе множество решений (2x = 5π/6 +2πk,  k ∈ Z) соответствует положительной второй производной. Здесь мы имеем точки минимума. Вычислим значения функции в найденных точках максимума и минимума: Данная функция представляет собой сумму линейной функции и косинуса. Такая комбинация приводит к тому, что максимумы и минимумы линейно возрастают с увеличением чисел n и k, как показано на рисунке 6.

   Пример 6

Определить экстремумы функции  f(x) = x² ln x. Заданная в условии функция определена и дифференцируема при x > 0. Найдем производную и определим стационарные точки функции в указанном интервале x: Корень x = 0 исключается из области допустимых значений. Поэтому рассмотрим второе решение: В левой окрестности точки  x = 1/√e  производная отрицательна, а в правой окрестности − положительна. Следовательно, функция имеет минимум в этой точке. Его значение составляет

   Пример 7

Найти экстремумы функции  f(x) = x⁴ − 8x³ +22x² − 24x + 1. Функция определена и дифференцируема на всем множестве действительных чисел ℜ. Следовательно, локальные экстремумы функции содержатся среди ее стационарных точек. Вычислим первую производную: Найдем стационарные точки: Подстановкой находим, что x = 1 является корнем кубического уравнения. Разделив кубическую функцию на x − 1, раскладываем ее на множители: Итак, найдено три "кандидата" в экстремумы функции. Для проверки этих точек воспользуемся вторым достаточным признаком экстремума. Вторая производная имеет вид: Подставляя координаты стационарных точек, находим значения второй производной: Отсюда следует, что x₁ = 1 и x₃ = 3 являются точками минимума, а x₂ = 2 − точкой максимума. В этих точках функция имеет следующие значения:

   Пример 8

Найти экстремумы функции Функция определена и дифференцируема при всех x ∈ ℜ. Находим производную и вычисляем стационарные точки функции: Тогда Определяем знаки производной методом интервалов (рисунок 7). В соответствии с первым достаточным признаком экстремума в точках x = −2 и x = 2 имеется максимум. В силу четности функции, значение функции в этих точках одинаковое: В точке x = 0 функция имеет минимум, равный

   Пример 9

Вывести закон Снеллиуса, описывающий преломление света на границе двух сред. Закон преломления света был установлен в 1621 году голландским физиком и математиком Виллебродом Снеллом (Снеллиусом) (1580-1626) и позже независимо французским ученым Рене Декартом (1596-1650).

В 1657 году французский математик Пьер де Ферма (1601-1665) вывел этот закон, используя принцип наименьшего действия. Это была одна из первых задач вариационного исчисления. В то время производные еще не были известны, и Ферма использовал для доказательства собственный метод анализа бесконечно малых величин (adequality). Теперь эта задача легко решается с помощью производной. Согласно принципу наименьшего действия Ферма, между любыми двумя точками реализуется такая траектория света, которая соответствует наименьшему времени распространения.

Рассмотрим две среды с плоской границей между ними (см. выше рисунок 8). Пусть свет распространяется из точки A в точку B, причем в первой среде угол падения (угол между падающим лучом и нормалью к границе раздела сред) составляет α₁, а во второй среде угол выходит под углом α₂. Скорости света в первой и второй среде равны, соответственно, v₁ и v₂.

Пусть луч пересекает границу между средами в точке с координатой x. Задача состоит в том, чтобы определить значение x, при котором время распространения света будет наименьшим.

Если y-координата точки A равна y₁, то время прохождения сигнала в первой среде равно . Аналогично, время прохождения сигнала во второй среде выражается формулой , где через L обозначена x-координата точки B.

Полное время распространения света представляет собой функцию от x: Определим экстремум этой функции. Производная имеет вид: Поскольку то экстремум существует при таком значении x = x₀, когда Производная t'(x) в левой окрестности критической точки x₀ отрицательна, а справа − положительна. Следовательно, точка экстремума является точкой минимума. Таким образом, мы получили закон преломления света, который записывается в виде

   Пример 10

Найти экстремумы функции Функция определена и дифференцируема при x ≤ 1. Найдем производную: Определим критические точки: Таким образом, мы имеем одну стационарную точку x = 3/4 и одну критическую точку x = 1 (в которой производная не существует).

Исследуем стационарную точку x = 3/4. В левой окрестности этой точки производная положительна, а в правой − отрицательна, т.е. здесь мы имеем дело с локальным максимумом. Его значение равно Что касается критической точки x = 1, то она существует на границе области определения, поэтому в ней локального экстремума быть не может.

   Пример 11

Найти экстремумы функции Вычислим производную и найдем критические точки функции: Как видно, функция имеет две стационарные точки x = 0, x = 4 (где производная равна нулю) и одну критическую точку x = 2 (в которой производная не существует).

Исследуем изменение знака производной при переходе через эти точки (рисунок 11). Таким образом, в точке x = 0 существует максимум. Его значение составляет А в точке x = 4 функция имеет минимум, равный В точке x = 2 функция терпит разрыв, и здесь экстремума не существует.

Схематический вид данной функции приведен на рисунке 12.

   Пример 12

Найти экстремумы функции Функция определена и дифференцируема на всем множестве ℜ. Находим ее стационарные точки: Для определения типа экстремума в этих точках воспользуемся вторым достаточным признаком. Вычислим вторую производную: Подставляя стационарные точки x = −1, x = 1, находим: Итак, точка x = −1 является точкой максимума, а точка x = 1 − точкой минимума. Соответствующие значения функции в них равны:

   Пример 13

Определить экстремумы неявной функции, заданной уравнением  x² + y² − 3xy + 5 = 0. Начнем анализ с вычисления производной неявной функции. Дифференцируя обе части уравнения по x, получаем: Как видно, производная обращается в бесконечность когда  3x − 2y = 0,  т.е.  y = 3x/2. Это происходит в следующих критических точках: Исследуем область допустимых значений функции y(x). Заданное уравнение можно переписать в виде Чтобы выразить y(x) в явном виде, надо решить квадратное уравнение, дискриминант которого равен Ясно, что функция y(x) существует при условии  x² ≥ 4. Отсюда следует, что критические точки  x = ±2  находятся на границе области определения функции y(x) и в них, по определению, экстремума быть не может.

Найдем теперь внутри области определения функции стационарные точки (в которых производная y'(x) равна нулю): Подставляя выражение для y в исходное уравнение, получаем: Итак, мы имеем две стационарные точки: Тип экстремума в данных точках удобнее определить, используя второй достаточный признак. Вычисляем вторую производную: Подставляя координаты стационарных точек, находим: Следовательно, точка (−3, −2) является максимумом неявной функции, а точка (3, 2) − ее минимумом. Данная функция представляет собой гиперболу и ее схематический вид показан на рисунке 13.

   Пример 14

Определить экстремумы функции Функция определена и дифференцируема при всех действительных x ≠ 0. Найдем производную и вычислим стационарные точки функции: Найдем вторую производную: Подставляя  x = ±1,  вычисляем знак второй производной в этих точках: По второму достаточному признаку экстремума получаем, что x = −1 является точкой максимума, а x = 1 − точкой минимума. Значения функции в указанных точках равны: Схематический вид функции представлен выше на рисунке 14.

   Пример 15

Определить экстремумы функции  f(x) = x ln²x. Функция определена и дифференцируема при x > 0. Найдем стационарные точки функции: Уравнение имеет два решения: Для определения характера найденных стационарных точек удобно воспользоваться вторым достаточным признаком экстремума. Вычислим вторую производную: В точках  x = 1  и  x = 1/e²  вторая производная имеет следующие значения: Таким образом, функция имеет минимум в точке  x = 1  и максимум в точке  x = 1/e².  Вычислим минимальное и максимальное значения функции: Данная функция схематически изображена на рисунке 15.