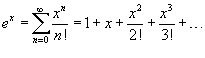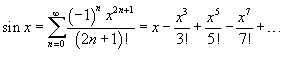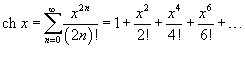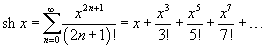|
Ряды Тейлора и Маклорена
|
|
Если функция
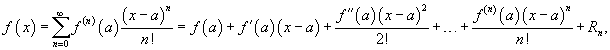 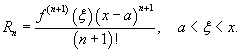 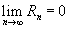 , то оно называется рядом Тейлора, представляющим разложение функции , то оно называется рядом Тейлора, представляющим разложение функции Если 
Разложение некоторых функций в ряд Маклорена
|
|
Пример 1
|
|
Найти ряд Маклорена для функции
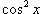 . .
Решение. 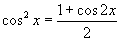 . .Поскольку ряд Маклорена для 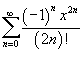 , то можно записать , то можно записать
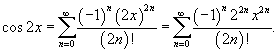 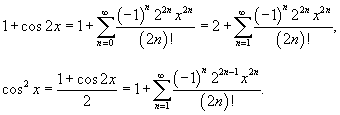 |
|
Пример 2
|
|
Разложить в ряд Тейлора функцию
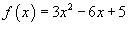 в точке в точке Решение. 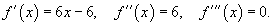  для всех для всех 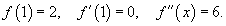 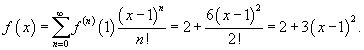 |
|
Пример 3
|
|
Найти разложение в ряд Маклорена функции
Решение. 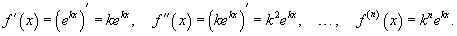 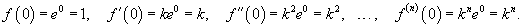 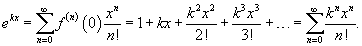 |
|
Пример 4
|
|
Найти разложение в ряд Тейлора кубической функции x3 в точке
Решение. 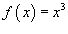 . Тогда . Тогда
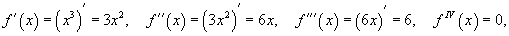 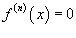 для всех для всех В точке 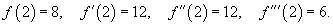 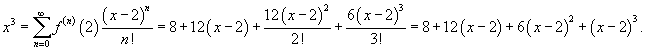 |
|
Пример 5
|
|
Найти разложение в ряд Маклорена функции
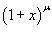 . .
Решение.
Пусть 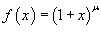 , где μ − действительное число, и , где μ − действительное число, и 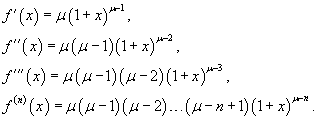 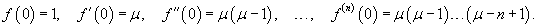 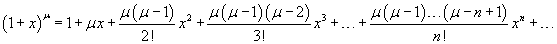 |
|
Пример 6
|
|
Найти разложение в ряд Маклорена функции
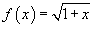 . .
Решение.
Используя формулу биномиального ряда, найденную в предыдущем примере, и подставляя 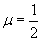 , получаем , получаем
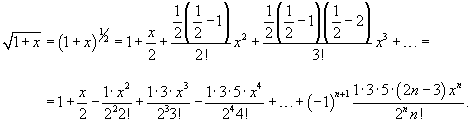 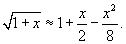 |