Биномиальный ряд представляет собой разложение в ряд Маклорена функции (1 + x)ⁿ и в общем случае записывается в виде

где 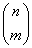− биномиальные коэффициенты, m − целое число, x − действительная (или комплексная) переменная, n − действительный (или комплексный) показатель степени.

Биномиальные коэффициенты выражаются формулой

Биномиальный ряд сходится при следующих условиях (предполагается, что x и n − действительные числа):
       •  −1 < x < 1, если n < −1;
       •  −1 < x ≤ 1, если −1 < n < 0;
       •  −1 ≤ x ≤ 1, если n > 0.

Бином Ньютона
В случае целых степеней n биномиальный ряд представляет собой конечную сумму n + 1 слагаемых и называется биномом Ньютона:

Биномиальные коэффициенты как число сочетаний
Коэффициенты в формуле бинома Ньютона равны числу неупорядоченных сочетаний из n по m элементов:

При такой записи бином Ньютона выражается формулой

Некоторые часто встречающиеся биномиальные разложения: