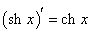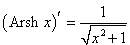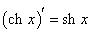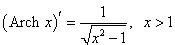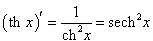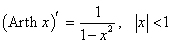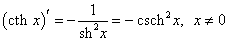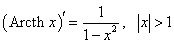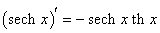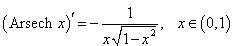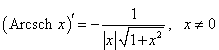|
Производные гиперболических функций
|
||||||||||||
|
Производные гиперболических функций
Производные гиперболических функций легко находятся, поскольку гиперболические функции являются комбинациями 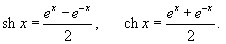 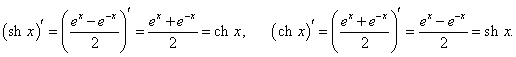 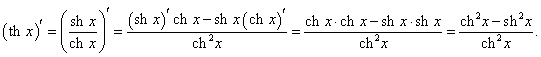 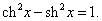 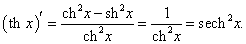 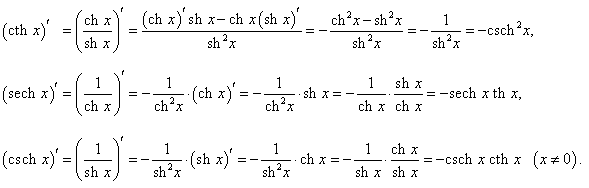 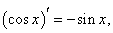 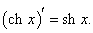 
Производные обратных гиперболических функций
Рассмотрим теперь производные 6 обратных гиперболических функций. Соответствующие формулы можно вывести, используя теорему о производной обратной функции.Возьмем, к примеру, функцию y = f (x) = Arsh x (обратный гиперболический синус). Вместе с функцией x = φ(y) = sh y они образуют пару взаимно-обратных функций. Тогда производная обратного гиперболического синуса равна 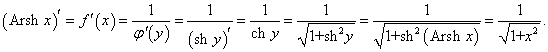 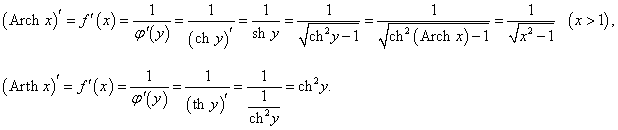  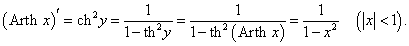 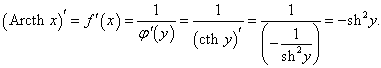 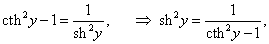 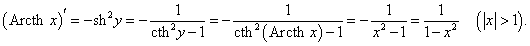 Выведем также производные обратного гиперболического секанса и косеканса, хотя эти функции встречаются достаточно редко. В соответствии с описанной схемой запишем две взаимно-обратные функции: y = f (x) = Arsech x, (x ∈ (0, 1]) и x = φ(y) = sech y, (y > 0). Вычислим производную: 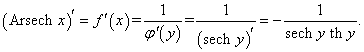 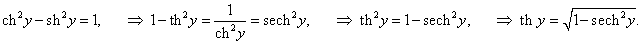 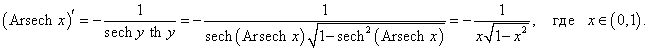 Рассмотрим сначала ветвь x > 0. В этом случае переменная y принимает значения y > 0 (графики данных функций можно посмотреть на странице Функции и их графики). Производная обратного гиперболического косеканса выражается в виде 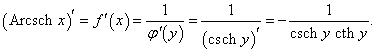 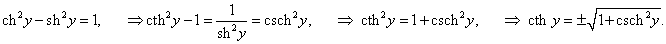 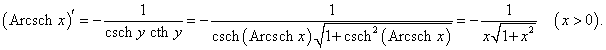 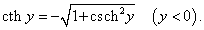 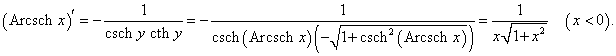 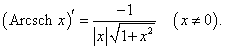
Таблица производных гиперболических функций
Для удобства соберем формулы производных всех гиперболических функций в одной таблице:
|
||||||||||||
|
Пример 1
|
||||||||||||
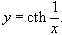
Решение.
Дифференцируя как сложную функцию, находим:
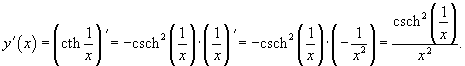 |
||||||||||||
|
Пример 2
|
||||||||||||
|
y = ln (sh x), x > 0.
Решение.
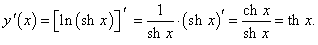 |
||||||||||||
|
Пример 3
|
||||||||||||
|
y = sh (tan x).
Решение.
Дифференцируя как сложную функцию, получаем:
 |
||||||||||||
|
Пример 4
|
||||||||||||
|
y = th (x2).
Решение.
Дифференцируя как сложную функцию, получаем:
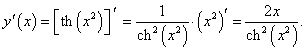 |
||||||||||||
|
Пример 5
|
||||||||||||
|
y = x sh x − ch x.
Решение.
Применяя правила дифференцирования разности и произведения функций, имеем:
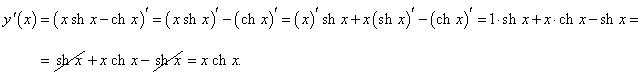 |
||||||||||||
|
Пример 6
|
||||||||||||
|
y = sh2 x.
Решение.
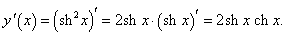  |
||||||||||||
|
Пример 7
|
||||||||||||
|
y = sh x th x.
Решение.
Используя правило дифференцирования произведения двух функций, получаем:
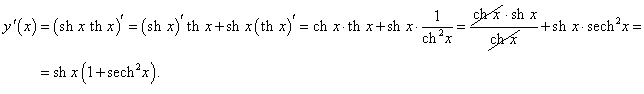 |
||||||||||||
|
Пример 8
|
||||||||||||
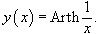
Решение.
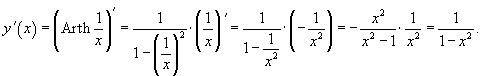 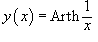 и и 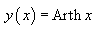 одинаковы. одинаковы. |
||||||||||||
|
Пример 9
|
||||||||||||
|
y = Arth (cos x).
Решение.
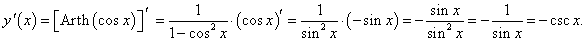 |
||||||||||||
|
Пример 10
|
||||||||||||
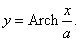
Решение.
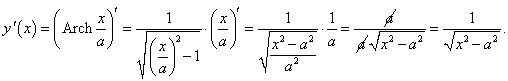 |
||||||||||||
|
Пример 11
|
||||||||||||
|
y = csch2 (3x).
Решение.
Дважды применяя правило дифференцирования сложной функции, получаем:
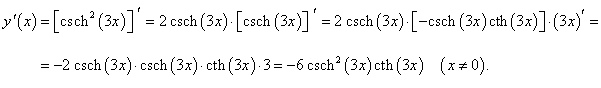 |
||||||||||||
|
Пример 12
|
||||||||||||
|
y = Arsh (tan x).
Решение.
Используя правило дифференцирования сложной функции, получаем:
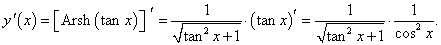 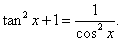 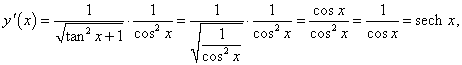 |
||||||||||||
|
Пример 13
|
||||||||||||
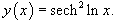
Решение.
Аналогично, применяя правило дифференцирования сложной функции, получаем:
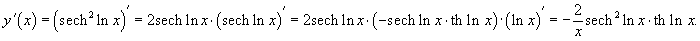 |
||||||||||||
|
Пример 14
|
||||||||||||
|
Доказать равенство
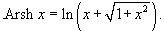 Решение. 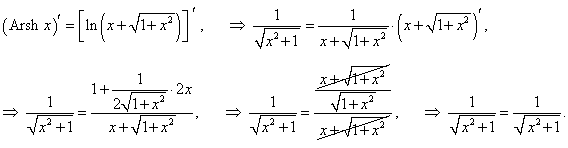 |
||||||||||||
|
Пример 15
|
||||||||||||

Решение.
Используя формулу производной сложной функции, можно записать:
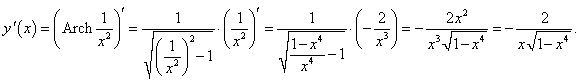 |
||||||||||||
|
Пример 16
|
||||||||||||
|
y = Arth (2√x).
Решение.
По правилу дифференцирования сложной функции
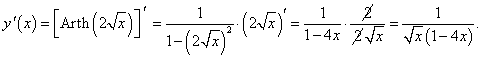  |
||||||||||||
|
Пример 17
|
||||||||||||
|
y = arctan (th x).
Решение.
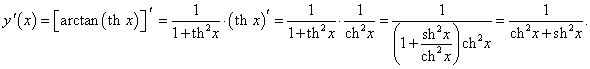 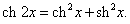 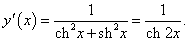 |
||||||||||||
|
Пример 18
|
||||||||||||
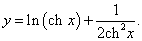
Решение.
Используя линейные свойства производной и правило дифференцирования сложной функции, имеем:
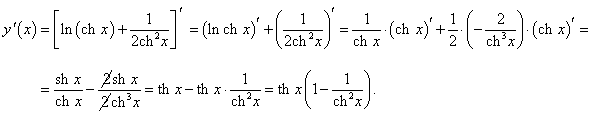 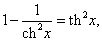 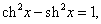 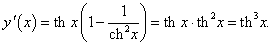 |
||||||||||||
|
Пример 19
|
||||||||||||
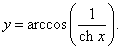
Решение.
Дважды применяя правило дифференцирования сложной функции, получаем:
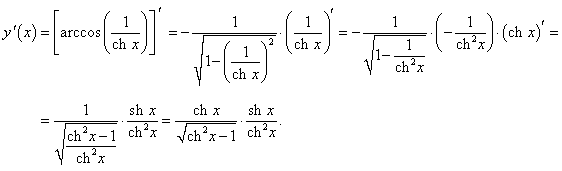 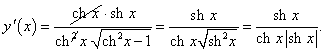 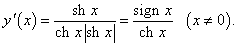 |
||||||||||||
|
Пример 20
|
||||||||||||

Решение.
Исследуем сначала область определения данной функции:
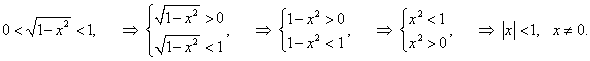 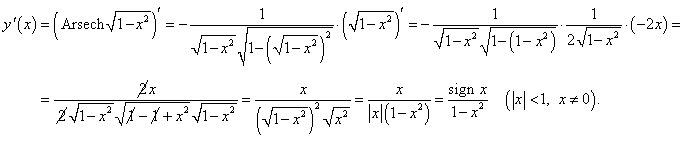 |
||||||||||||