|
Неоднородные дифференциальные уравнения второго порядка с переменными коэффициентами
|
|
Определение и общая схема решения
Линейное неоднородное уравнение второго порядка с переменными коэффициентами имеет вид
 Соответствующее однородное уравнение записывается в виде  
Метод вариации постоянных
Метод вариации постоянных (или метод Лагранжа) используется для построения общего решения неоднородного уравнения, когда известно общее решение ассоциированного с ним однородного уравнения.Пусть общее решение однородного уравнения 2-го порядка выражается через фундаментальную систему решений  Производные неизвестных функций   Далее, зная производные  Тогда общее решение исходного неоднородного уравнения будет выражаться формулой   |
|
Пример 1
|
|
Найти общее решение дифференциального уравнения
Решение.       Теперь воспользуемся методом вариации постоянных и построим общее решение неоднородного уравнения. Будем рассматривать параметры C1 и C2 как функции от переменной x. Производные этих функций определяются из системы уравнений   во втором уравнении записана после преобразования исходного дифференциального уравнения в стандартную форму: во втором уравнении записана после преобразования исходного дифференциального уравнения в стандартную форму:
  В результате получаем общее решение неоднородного уравнения в виде  |
|
Пример 2
|
|
Найти общее решение неоднородного дифференциального уравнения
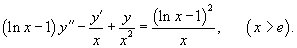 Решение. 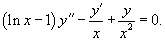 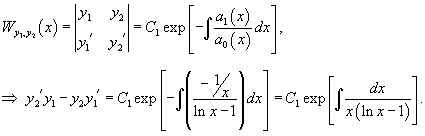 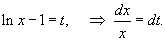 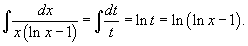 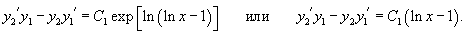 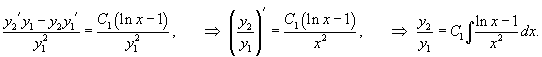 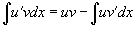 . Обозначим . Обозначим
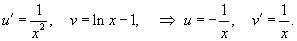 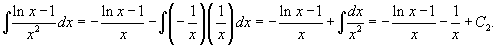 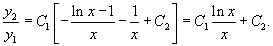 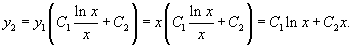 Теперь, используя метод вариации постоянных, найдем общее решение неоднородного уравнения, которое в стандартном виде записывается как 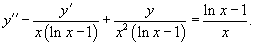  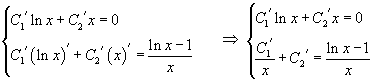 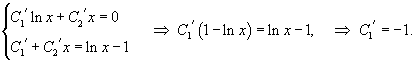 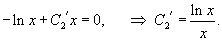 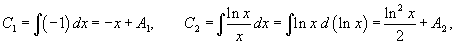 Итак, общее решение исходного неоднородного уравнения имеет вид: 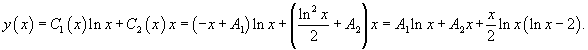 |
|
Пример 3
|
|
Найти общее решение неоднородного дифференциального уравнения
Решение. 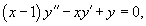 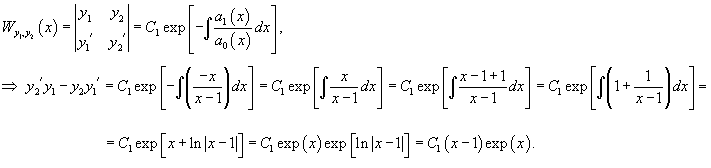 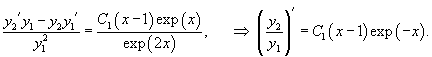 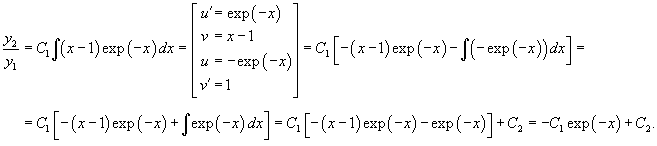 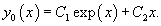 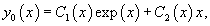 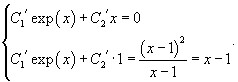 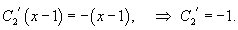 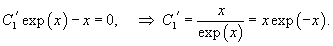 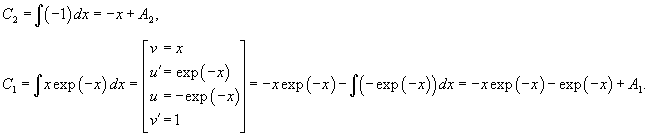 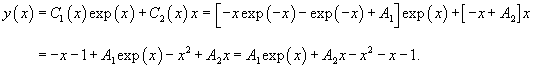 |