|
Однородные дифференциальные уравнения второго порядка с переменными коэффициентами
|
|
Линейное однородное уравнение второго порядка с переменными коэффициентами записывается в виде

Линейная независимость функций. Определитель Вронского
Функции  Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функции   , эти функции будут линейно зависимыми. , эти функции будут линейно зависимыми.Пусть n функций  Теорема. Если система функций Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка
Фундаментальная система решений
Совокупность двух линейно независимых частных решений линейного однородного дифференциального уравнения второго порядка образует его фундаментальную систему решений.Если  Заметим, что по заданной фундаментальной системе решений 
Формула Лиувилля-Остроградского
Итак, как указано выше, общее решение однородного дифференциального уравнения второго порядка является линейной комбинацией двух линейно независимых частных решений Очевидно, что частные решения зависят от коэффициентов дифференциального уравнения. Формула Лиувилля-Остроградского устанавливает связь между вронскианом Пусть   справедлива формула Лиувилля-Остроградского: справедлива формула Лиувилля-Остроградского:

Практические методы решения однородных уравнений 2-го порядка с переменными коэффициентами
К сожалению, общего метода отыскания частного решения не существует. Обычно это можно сделать путем подбора.Если известно частное решение Другой способ понижения порядка основан на использовании формулы Лиувилля-Остроградского. Здесь также одно частное решение |
|
Пример 1
|
|
Исследовать, являются ли функции
Решение.  |
|
Пример 2
|
|
Найти определитель Вронского для системы функций
Решение. 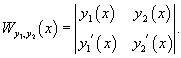 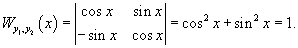 |
|
Пример 3
|
|
Составить линейное однородное дифференциальное уравнение, если известна его фундаментальная система решений: x,
Решение. 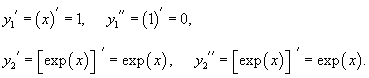 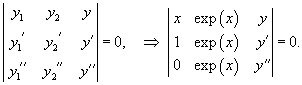 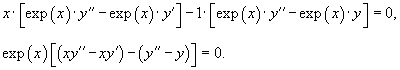 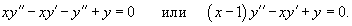 |
|
Пример 4
|
|
Найти общее решение уравнения
Решение. 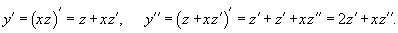 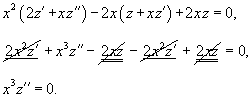 Отсюда находим функцию z: 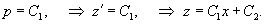 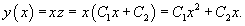 |
|
Пример 5
|
|
Найти общее решение уравнения
Решение. 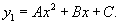 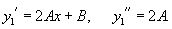 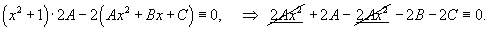 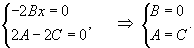 Сделаем следующую подстановку, чтобы понизить порядок уравнения: 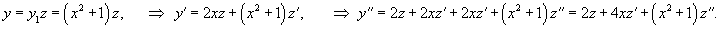 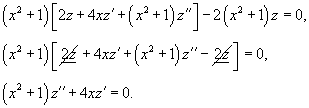 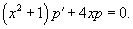 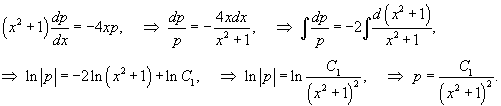 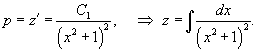 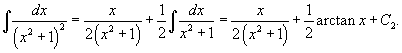 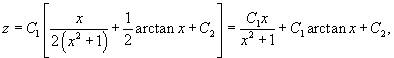 Таким образом, общее решение имеет вид: 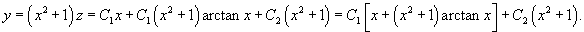 |
|
Пример 6
|
|
Найти общее решение уравнения
Решение. 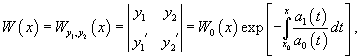 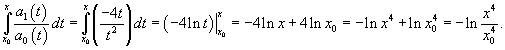 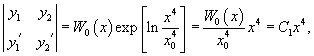 Поскольку частное решение y1 известно, то мы получили дифференциальное уравнение первого порядка для определения другого частного решения y2. После деления на y12 имеем: 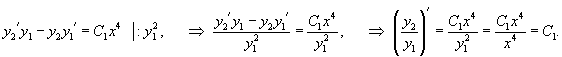 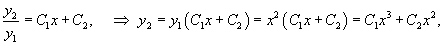 |
|
Пример 7
|
|
Найти по формуле Лиувилля-Остроградского общее решение уравнения
Решение. 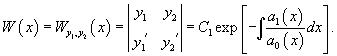 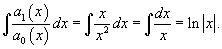 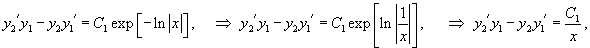 Делим обе части уравнения на 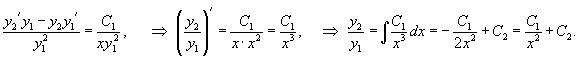 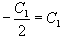 . Окончательный ответ выглядит так: . Окончательный ответ выглядит так:
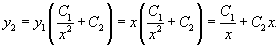 |