|
Интегрирование по частям
|
|
Пусть
   |
|
Пример 1
|
|
Вычислить интеграл
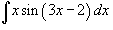 . .
Решение. 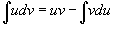 . Пусть . Пусть 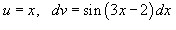 . Тогда . Тогда
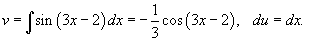 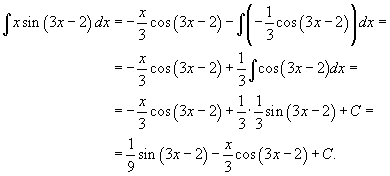 |
|
Пример 2
|
|
Проинтегрировать
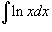 . .
Решение. Тогда 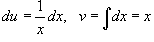 . Получаем . Получаем
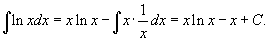 |
|
Пример 3
|
|
Вычислить интеграл
 . .
Решение. 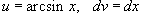 . Тогда . Тогда 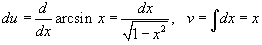 , так что интеграл переписывается в виде , так что интеграл переписывается в виде
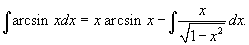 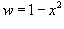 . В этом случае . В этом случае 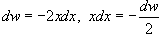 . .В результате последний интеграл становится равным 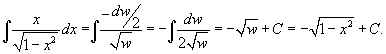 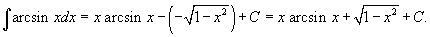 |
|
Пример 4
|
|
Вычислить интеграл
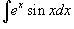 . .
Решение. 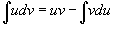 . Полагаем . Полагаем 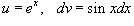 . Тогда . Тогда 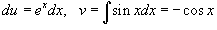 и интеграл записывается в виде и интеграл записывается в виде
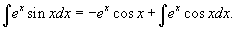 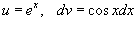 . Следовательно, . Следовательно, 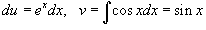 . Для первоначального интеграла получаем следующее уравнение: . Для первоначального интеграла получаем следующее уравнение:
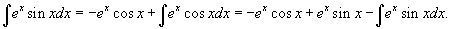 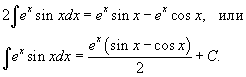 |
|
Пример 5
|
|
Вывести формулу редукции (понижения степени) для
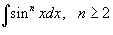 . .
Решение. 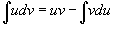 , полагаем , полагаем 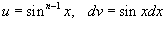 . Тогда . Тогда
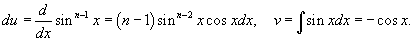 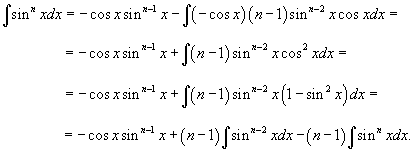 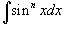 . Получаем . Получаем
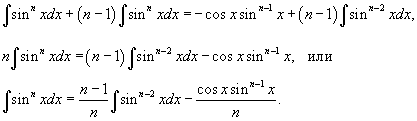 |