|
Линейные неоднородные системы дифференциальных уравнений с постоянными коэффициентами
|
|
Нормальную линейную неоднородную систему n уравнений с постоянными коэффициентами можно записать в виде
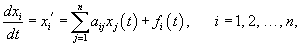 Введем следующие векторы: 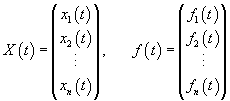  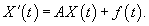 Общее решение X(t) неоднородной системы представляет собой сумму общего решения 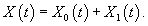 Еще одним важным свойством линейных неоднородных систем является принцип суперпозиции, который формулируется следующим образом: Если 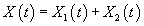 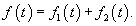
Метод исключения
Данный метод позволяет свести нормальную неоднородную систему n уравнений к одному уравнению n-го порядка. Этот способ удобно использовать для решения систем 2-го порядка.
Метод неопределенных коэффициентов
Метод неопределенных коэффициентов хорошо подходит для решения систем уравнений, неоднородная часть которых представляет собой квазимногочлен.Действительным векторным квазимногочленом называется вектор-функция вида 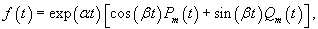 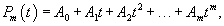 В случае, когда неоднородная часть f(t) является векторным квазимногочленом, то частное решение также будет представляться некоторым векторным квазимногочленом, похожим по структуре на f(t). Так, например, если неоднородная функция равна 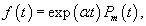 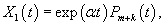 Аналогичные правила определения степени многочленов применяются и для квазимногочленов вида 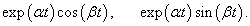 После выбора структуры частного решения
Метод вариации постоянных
В случае произвольной правой части f(t) общим методом решения является метод вариации постоянных (метод Лагранжа).Пусть общее решение однородной системы найдено и представляется в виде 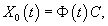 Заменим постоянные числа Ci на неизвестные функции 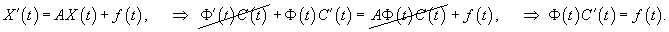 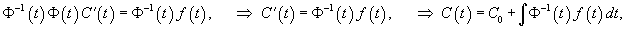 Тогда общее решение неоднородной системы можно записать как 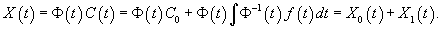 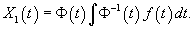 |
|
Пример 1
|
|
Решить систему уравнений методом исключения.
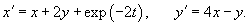
Решение.
Продифференцируем первое уравнение и подставим в него производную y' из второго уравнения:
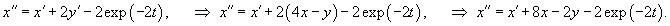 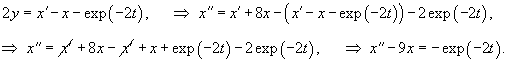 Решаем сначала однородное уравнение 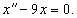 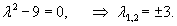 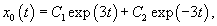 Учитывая вид неоднородной части в уравнении для x(t), будем искать частное решение 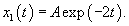 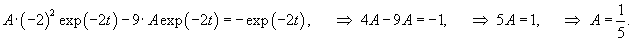 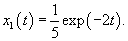 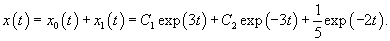 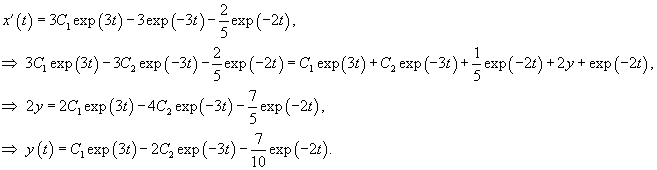 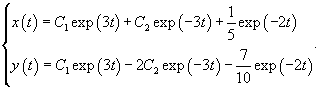 |
|
Пример 2
|
|
Решить систему уравнений методом неопределенных коэффициентов:
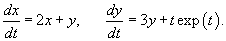
Решение.
Запишем данную систему в матричной форме:
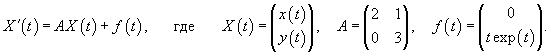 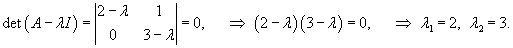 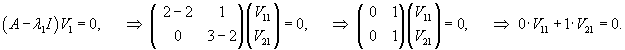 Аналогично найдем собственный вектор 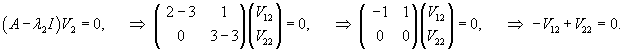 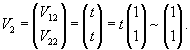 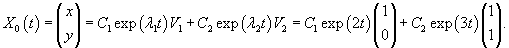 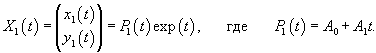 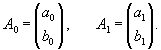 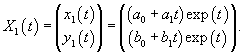 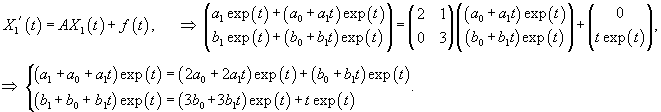 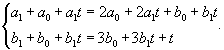 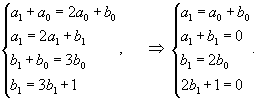 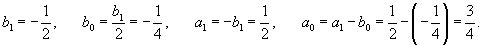 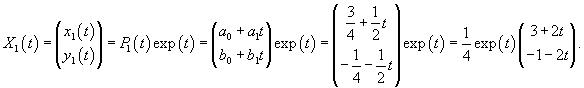 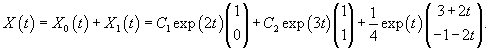 |
|
Пример 3
|
|
Решить систему уравнений методом неопределенных коэффициентов:
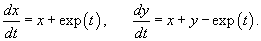
Решение.
Вычислим собственные значения λi матрицы A и построим общее решение однородной системы:
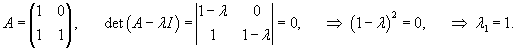 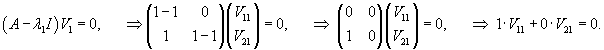 Второй линейно независимый вектор 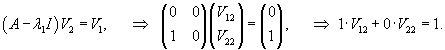 Общее решение однородной системы будет выражаться формулой 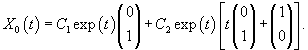 Как видно, длина жордановой цепочки для Теперь перейдем к определению частного решения Следовательно, частное решение 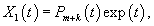 Итак, в данном случае нужно выбрать многочлен второй степени: 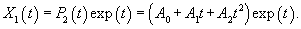 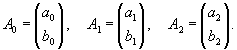 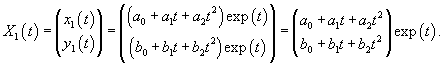 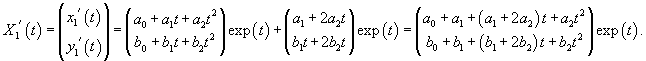 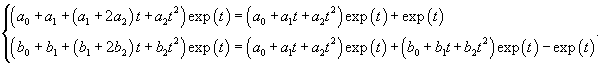 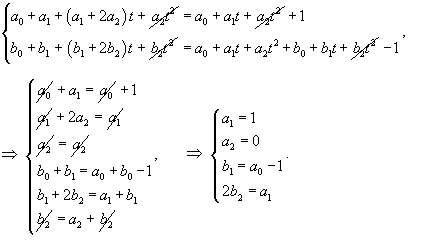 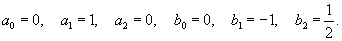 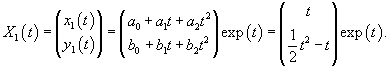 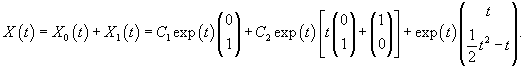 |
|
Пример 4
|
|
Решить систему линейных дифференциальных уравнений методом неопределенных коэффициентов:
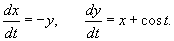
Решение.
Построим сначала общее решение однородной системы. Собственные значения матрицы A равны:
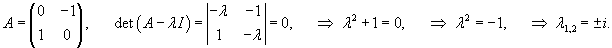 Вычислим собственный вектор 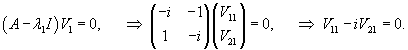 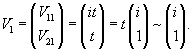 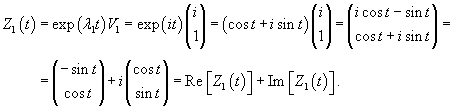 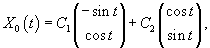 Определим теперь частное решение 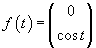 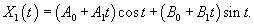 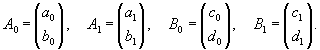 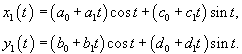 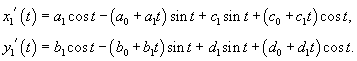 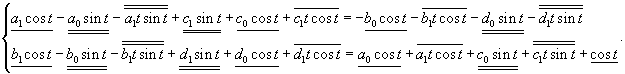  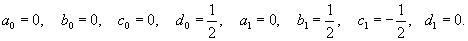 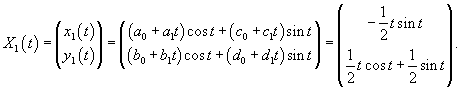 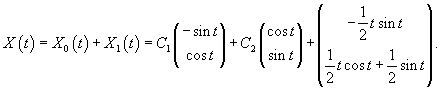 |
|
Пример 5
|
|
Решить систему уравнений методом вариации постоянных:
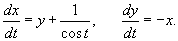
Решение.
Построим сначала общее решение однородной системы. Вычислим собственные значения:
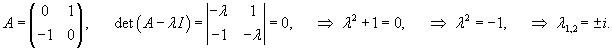 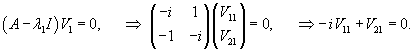 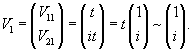 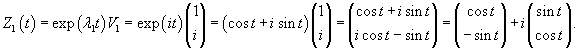 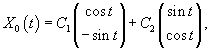 Запишем полученное решение отдельно для каждой координаты: 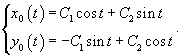 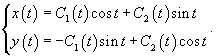 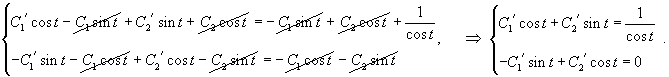 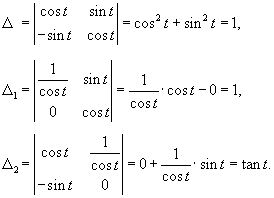 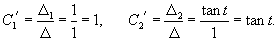 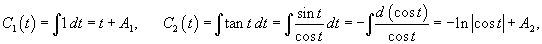 В результате получаем следующие выражения для 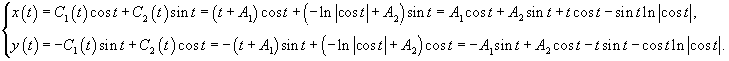 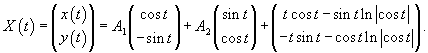 |
|
Пример 6
|
|
Решить линейную неоднородную систему методом вариации постоянных.
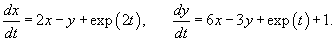
Решение.
Начнем с построения общего решения однородной системы. Вычислим собственные значения матрицы A и соответствующие им собственные векторы.
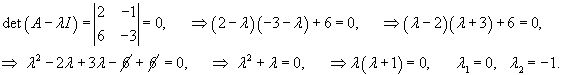 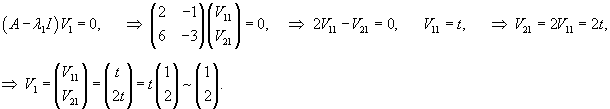 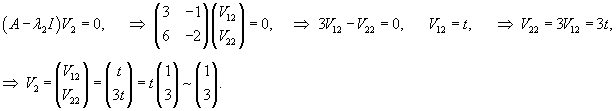 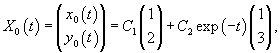 Рассмотрим исходную неоднородную систему и найдем ее решение методом вариации постоянных. Заменим постоянные числа C1, C2 на функции 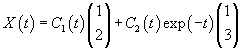 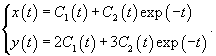 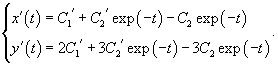 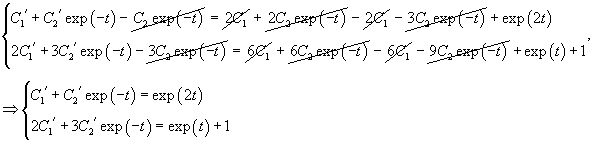  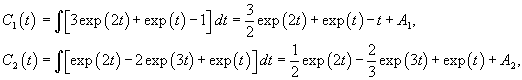 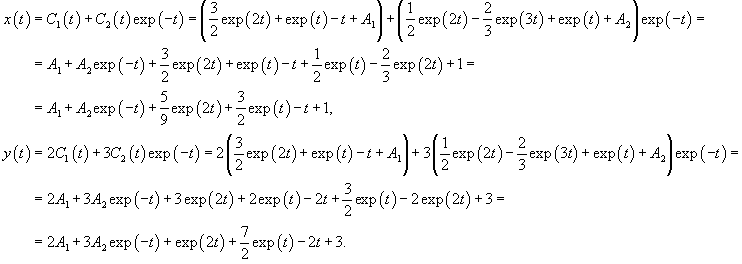 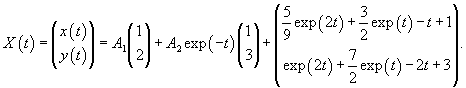 |