Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейное неоднородное уравнение данного типа имеет вид: где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение: Теорема: Общее решение неоднородного уравнения является суммой общего решения y₀(x) соответствуюшего однородного уравнения и частного решения y₁(x) неоднородного уравнения: Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений. Если общее решение y₀ ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.

Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид: Вместо постоянных C₁ и C₂ будем рассматривать вспомогательные функции C₁(x) и C₂(x). Будем искать эти функции такими, чтобы решение удовлетворяло неоднородному уравнению с правой частью f(x).

Неизвестные функции C₁(x) и C₂(x) определяются из системы двух уравнений: Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов.

Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

1. 
   
2. 
   где P_n(x) и Q_m(x) − многочлены степени n и m, соответственно.

В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения.

В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель x^s, где s − кратность корня α в характеристическом уравнении.

В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x.

Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение. Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

   Пример 1

Решить дифференциальное уравнение  y'' + y = sin(2x). Сначала мы решим соответствующее однородное уравнение  y'' + y = 0. В данном случае корни характеристического уравнения являтся чисто мнимыми: Следовательно, общее решение однородного уравнения определяется выражением Вернемся снова к неоднородному уравнению. Будем искать его решение в виде используя метод вариации постояных.

Функции C₁(x) и C₂(x) можно найти из следующей системы уравнений: Тогда Выразим производную C₁' (x) из первого уравнения: Подставляя во второе уравнение, находим производную C₂' (x): Отсюда следует, что Интегрируя выражения для производных C₁' (x) и C₂' (x), получаем: где A₁, A₂ − постоянные интегрирования.

Теперь подставим найденные функции 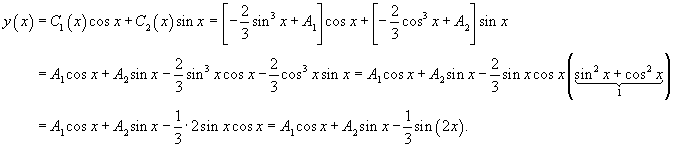C₁(x) и C₂(x) в формулу для y₁(x) и запишем общее решение неоднородного уравнения:

   Пример 2

Найти общее решение уравнения  y'' + y' −6y = 36x. Воспользуемся методом неопределенных коэффициентов. Правая часть заданного уравнения представляет собой линейную функцию  f(x) = ax + b. Поэтому будем искать частное решение в виде Производные равны: Подставляя это в дифференциальное уравнение, получаем: Последнее уравнение является тождеством, то есть справедливо для всех x, поэтому приравняем коэффициенты при слагаемых с одинаковыми степенями x в левой и правой части: Из полученной системы находим: A = −6, B = −1. В результате, частное решение записывается в виде Теперь найдем общее решение однородного дифференциального уравнения. Вычислим корни вспомогательного характеристического уравнения: Следовательно, общее решение соответствующего однородного уравнения имеет вид: Итак, общее решение исходного неоднородного уравнения выражается формулой

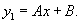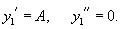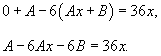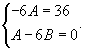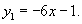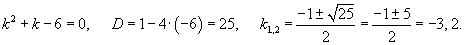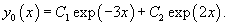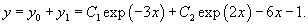   Пример 3

Решить дифференциальное уравнение  y'' − 5y' + 4y = exp(4x). Сначала решим соответствующее однородное уравнение  y'' − 5y' + 4y = 0. Корни характеристического уравнения равны: Следовательно, общее решение однородного уравнения записывается как где C₁, C₂ − постоянные числа.

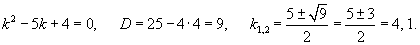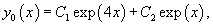Найдем теперь частное решение неоднородного дифференциального уравнения. Заметим, что показатель экспоненциальной функции в правой части совпадает с корнем 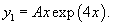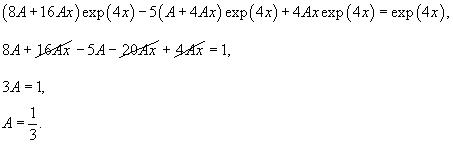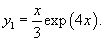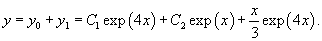k₁ = 4 характеристического уравнения. Поэтому будем искать частное решение в виде Производные равны: Подставляя функцию y₁ и ее производные в дифференциальное уравнение, получаем: Таким образом, частное решение имеет вид: Теперь можно записать полное решение неоднородного уравнения:

   Пример 4

Найти общее решение уравнения  y'' + 9y = 2x² − 5. Сначала определим общее решение соответствующего однородного уравнения. Вычислим корни характеристического уравнения: Следовательно, решение однородного уравнения записывается в виде: Построим теперь частное решение. Правая часть в заданном уравнении является квадратичной функцией. Поэтому попробуем найти частное решение в аналогичной форме: где числа A, B, C можно определить методом неопределенных коэффициентов. В результате получаем: Подставляем это в исходное неоднородное дифференциальное уравнение: Приравнивая коэффициенты при членах с одинаковыми степенями x, находим: Таким образом, частное решение определяется формулой Тогда общее решение исходного неоднородного дифференциального уравнения выражается в виде:

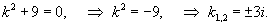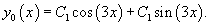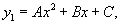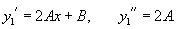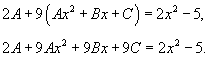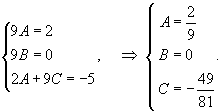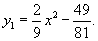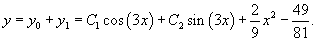   Пример 5

Решить дифференциальное уравнение  y'' + 16y = 2cos²x. Прежде всего, решим соответствующее однородное уравнение. Характеристическое уравнение имеет корни: так что общее решение однородного уравнения записывается в виде: Теперь найдем частное решение неоднородного уравнения. Представим правую часть как Отсюда следует, что частное решение определяется функцией где числа A, B и C можно вычислить, используя метод неопределенных коэффициентов. Первая и вторая производные функции y₁ равны: Подставляя это в дифференциальное уравнение, находим: Последнее выражение является тождеством. Поэтому можно записать следующую систему уравнений для определения коэффициентов A, B, C: Следовательно, частное решение имеет вид: Соответственно, общее решение неоднородного уравнения записывается как

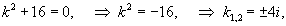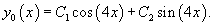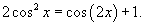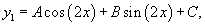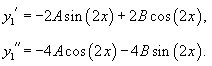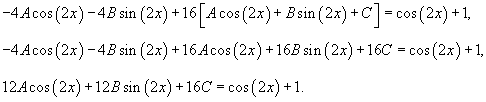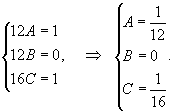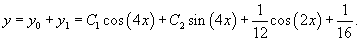   Пример 6

Решить уравнение  y'' + y = sec²x, используя метод вариации постоянных. Найдем решение соответствующего однородного уравнения  y'' + y = 0. Характеристическое уравнение имеет корни: Следовательно, общее решение однородного уравнения записывается в виде: Найдем теперь общее решение исходного неоднородного уравнения. В соответствии с методом вариации постоянных, будем рассматривать коэффициенты C₁ и C₂ как функции C₁(x) и C₂(x).

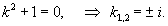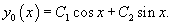Производные 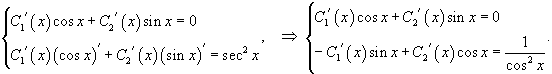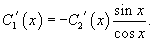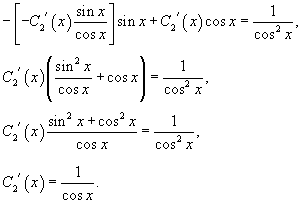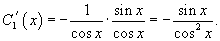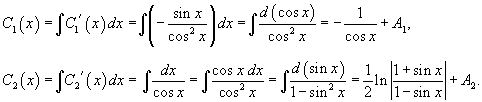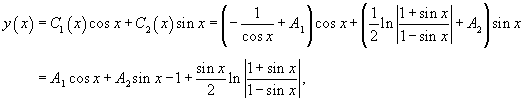C₁' (x), C₂' (x) определяются следующей системой уравнений: Из первого уравнения находим: Подставляя во второе уравнение, получаем: Следовательно, Интегрируем полученные выражения, чтобы найти функции C₁(x), C₂(x): В результате находим, что общее решение неоднородного уравнения представляется в виде: где A₁, A₂ − постоянные числа.

   Пример 7

Найти решение дифференциального уравнения  y'' − 7y' +12y = 8sinx + exp(3x). Рассмотрим соответствующее однородное уравнение  y'' − 7y' +12y = 0. Корни вспомогательного характеристического уравнения равны: Следовательно, общее решение однородного уравнения определяется выражением: Видно, что правая часть представляет собой сумму двух функций. Согласно принципу суперпозиции, частное решение можно представить в виде: где y₂(x) − частное решение дифференциального уравнения  y'' − 7y' +12y = 8sinx, а y₃(x) − частное решение дифференциального уравнения  y'' − 7y' +12y = exp(3x).

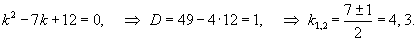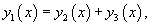Сначала определим функцию 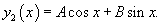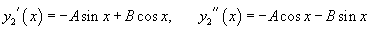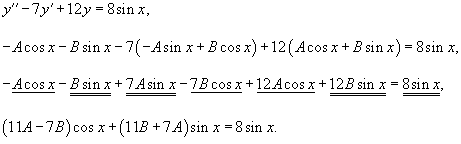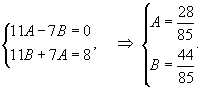y₂(x). В данном случае мы будем искать решение в форме Подставим функцию y₂(x) и ее производные в соответствующее дифференциальное уравнение: Следовательно, Тогда получаем:  y₂(x) = 2sinx.

Аналогично можно сконструировать частное решение 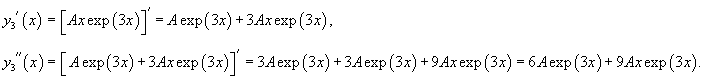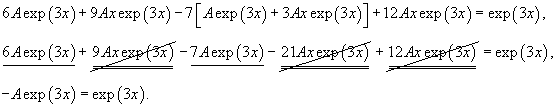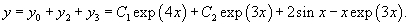y₃(x) для уравнения  y'' − 7y' +12y = exp(3x). Заметим, что здесь показатель степени в экспоненциальной функции совпадает с корнем k₂ = 3 характеристического уравнения соответствующего однородного уравнения. Поэтому, мы будем искать частное решение в форме Производные имеют вид: Подставляем функцию y₃(x) и ее производные в дифференциальное уравнение: Как видно, A = −1. Следовательно, частное решение y₃(x) можно записать в виде: В результате, общее решение исходного неоднородного уравнения определяется выражением