Наибольшее и наименьшее значения функции

Рассмотрим функцию y = f(x), которая является непрерывной на отрезке [a, b]. Если существует точка x₀∈ [a, b], такая, что для всех  x ∈ [a, b]  выполняется неравенство  f(x) ≤ f(x₀) , то говорят, что функция f(x) принимает в точке x₀ наибольшее (максимальное) значение на отрезке [a, b].

Наибольшее значение функции f(x) на отрезке [a, b] является одновременно точной верхней гранью множества значений функции на этом отрезке и обозначается как Аналогично, если существует точка x₀∈ [a, b], такая, что для всех  x ∈ [a, b]  выполняется неравенство  f(x) ≥ f(x₀) , то функция f(x) принимает в точке x₀ наименьшее (минимальное) значение на отрезке [a, b].

Наименьшее значение функции f(x) на отрезке [a, b] является также точной нижней гранью множества значений функции на этом отрезке и записывается в виде Введенные понятия характеризуют поведение функции на конечном отрезке, в отличие от локального экстремума, который описывает свойства функции в малой окрестности точки. Поэтому наибольшее и наименьшее значения функции на отрезке часто называют также глобальным (абсолютным) максимумом или, соответственно, глобальным минимумом. Согласно второй теореме Вейерштрасса о непрерывных функциях, если функция f(x) непрерывна на отрезке [a, b], то она достигает на нем своей точной верхней и нижней грани.

Доказательство этой теоремы опирается на первую теорему Вейерштрасса, которая формулируется так:

Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на нем, т.е. существует число M, такое, что |f(x)| ≤ M  для всех  x ∈ [a, b].

Возвращаясь ко второй теореме Вейерштрасса, обозначим через M точную верхнюю грань множества значений функции (или наибольшее значение функции) на отрезке [a, b]. Предположим противное − что точная верхняя грань не достигается, т.е. допустим, что Рассмотрим вспомогательную функцию: Поскольку знаменатель не равен нулю, то функция φ(x) также непрерывна на [a, b] и, следовательно, по первой теореме Вейерштрасса ограничена на этом отрезке:  φ(x) ≤ L,  где  L > 0. Отсюда получаем, что Другими словами, число будет являться точной верхней гранью функции f(x), что противоречит условию. (По условию, точная верхняя грань функции равна M.)

Таким же образом можно доказать, что непрерывная на отрезке [a, b] функция достигает свой точной нижней грани (или наименьшего значения).

Итак, согласно второй теореме Вейерштрасса, непрерывная на отрезке функция всегда достигает своего наибольшего и наименьшего значения на этом отрезке. Пусть функция y = f(x) непрерывна на отрезке [a, b].

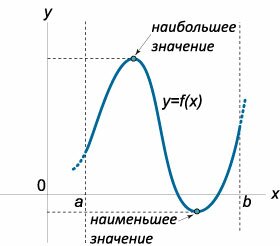
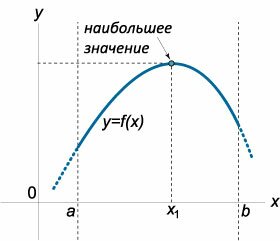
Если функция на этом отрезке имеет локальные максимумы в точках  x₁, x₂, ..., x_n ,  то наибольшее значение функции f(x) на отрезке [a, b] равно наибольшему из чисел Аналогично, если функция на этом отрезке имеет локальные минимумы в точках   x₁, x₂, ..., x_k ,  то наименьшее значение функции f(x) на отрезке [a, b] равно наименьшему из чисел Таким образом, наибольшее (наименьшее) значения функции могут достигаться либо на границе отрезка (рисунок 1), либо в точках локального экстремума внутри отрезка (рисунок 2). 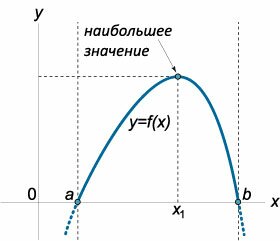Если внутри отрезка [a, b] существует единственная точка экстремума x₁ и эта точка является локальным максимумом (минимумом), то в ней функция принимает наибольшее (наименьшее) значение (рисунок 3). 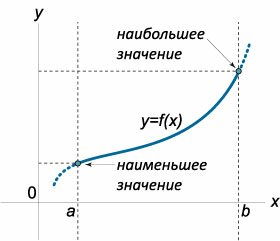Если функция y = f(x) не имеет критических точек на отрезке [a, b], то функция принимает наименьшее значение на одном конце отрезка и наибольшее значение − на другом (рисунок 4). На практике часто встречается случай, когда на отрезке [a, b] задана дифференцируемая и положительно определенная функция  f(x) > 0, причем в граничных точках она равна нулю:  f(a) = f(b) = 0.  Если такая функция имеет единственную стационарную точку x₁ (где  f '(x₁) = 0), то эта точка является не только локальным максимумом функции, но и ее наибольшим значением на отрезке [a, b] (рисунок 5). В примерах 1-10 найти наибольшее и наименьшее значения функции на заданном отрезке.

   Пример 1

       f(x) = x² − 2x + 5,    x ∈ [−1, 4]. Данная функция определена и дифференцируема при всех x ∈ ℜ. Определим стационарные точки: Найденная точка локального экстремума принадлежит интервалу (−1, 4). Вычислим значения функции в точке x = 1 и на концах отрезка: Следовательно, наибольшее значение функции равно  f(4) = 13,  а наименьшее значение составляет  f(1) = 4.

   Пример 2

Данная функция не определена при  x = 0,  но эта точка не входит в заданный отрезок. Дифференцируя функцию, находим точки экстремума: В отрезок [0.5, 2] попадает лишь точка  x = √2.  Вычислим значения функции в точке экстремума  x = √2  и в граничных точках отрезка: Итак, наибольшее значение функции на данном отрезке равно  4.5  в точке  x = 0.5,  и наименьшее значение составляет  2.83  при  x = √2.

   Пример 3

       f(x) = 3x⁴ − 6x² + 2,    x ∈ [−2, 2]. Данная функция определена и дифференцируема на всей числовой оси. В таком случае все локальные экстремумы находятся из уравнения  f '(x) = 0: Как видно, функция имеет три локальных экстремума, причем все эти точки попадают в заданный отрезок [−2, 2]. Рассчитаем значения функции в точках экстремума и на концах отрезка: Поскольку функция является четной, то следовательно: Итак, функция принимает наименьшее значение  −1 сразу в двух точках: при x = −1 и x = −1. Наибольшее значение 26 достигается также в двух точках: при x = −2 и x = −2. Схематический график функции показан на рисунке 7.

   Пример 4

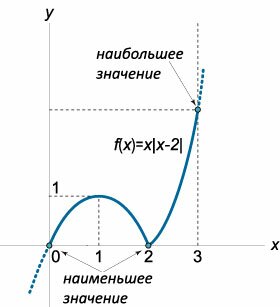
       f(x) = x|x − 2|,    x ∈ [0, 3]. Раскрывая модуль, представим данную функцию в виде Как видно, функция состоит из двух квадратичных функций  f₁(x) = −x² + 2x  и  f₂(x) = x² − 2x.  В точке x = 2, где соединяются обе ветви, график функции имеет излом (рисунок 8), т.е. в этой точке производной не существует.

Найдем другие критические точки обеих ветвей функции: Здесь корень x = 1 имеет смысл лишь для первой ветви решений, которая существует при x < 2.

Определим значения функции в найденных критических точках x = 1, x = 2 и на концах отрезка при x = 0 и x = 3: Отсюда видно, что функция принимает наименьшее значение y = 0 в двух точках: при x = 0 и x = 2. Наибольшее значение составляет  f(3) = 3.

   Пример 5

       f(x) = √3 −2x,    x ∈ [−3, 1]. Функция определена при условии Заданный в условии отрезок попадает в область определения функции. На этом отрезке функция дифференцируема и ее экстремумы (если они существуют) определяются из условия  f '(x) = 0.  Найдем производную: Отсюда следует, что уравнение  f '(x) = 0  не имеет решений, т.е. функция не имеет локальных экстремумов. Так как производная отрицательна, то функция f(x) монотонно убывает на отрезке [−3, 1]. Вычисляя значение функции в граничных точках: находим, что наибольшее значение равно 3 при x = −3, а наименьшее значение равно 1 при x = 1.

   Пример 6

Видно, что функция определена и дифференцируема при всех x ∈ ℜ. Поэтому все критические точки находятся из условия  f '(x) = 0: Найдено 2 точки локального экстремума:  x₁ = 0  и  x₂ = 2/ln 2.  Вычислим значения функции в этих точках и на границах отрезка и определим наибольшее и наименьшее значения функции на заданном отрезке: Следовательно, наибольшее значение функции равно 2 при x = −1, наименьшее значение равно 0 при x = 0.

   Пример 7

Данная функция определена и дифференцируема при x > 0. Ее производную можно найти с помощью логарифмического дифференцирования: Приравнивая производную нулю, определим критические (точнее стационарные) точки функции: Вычислим теперь значения функции в критической точке  x = e  (которая попадает в заданный отрезок) и на границах отрезка − в точках x = 2 и x = 3: Итак, наименьшее значение функции равно  f(2) ≈ 1.414,  а наибольшее значение, соответственно, равно  f(e) ≈ 1.445

   Пример 8

       f(x) = cos²x − 2sin x,    x ∈ [0, 2π]. Производная функции имеет вид: Найдем критические точки, полагая  f '(x) = 0: В заданный отрезок [0, 2π] попадают следующие критические точки: Теперь достаточно вычислить значения функции в этих точках и на краях отрезка, чтобы определить наибольшее и наименьшее значения: Функция имеет период 2π. Поэтому  f(2π) = f(0) = 1. 

Таким образом наибольшее значение функции на отрезке [0, 2π] равно 2 при  x = 3π/2 , а наименьшее − равно −2 при  x = π/2 .

   Пример 9

Очевидно, функция определена всюду на числовой оси, кроме точки x = −1, которая не попадает в заданный интервал. Находим производную: Как видно, производная нигде не равна нулю. Поэтому других критических точек, кроме x = −1, у функции не существует. Следовательно, функция является монотонно убывающей (учитывая, что производная отрицательна всюду в области определения). В таком случае наибольшее и наименьшее значения функции достигаются на границах отрезка: Наименьшее значение равно  f(1) = 0,  а наибольшее значение составляет  f(0) = π/4.

   Пример 10

Поскольку функция f(x) всюду неотрицательна, то наименьшее значение равно 0 и достигается на отрезке [0, π] в следующих критических точках: Чтобы определить наибольшее значение, вычислим производную данной функции: Критические точки x = π/3, x = 2π/3, в которых выполняется равенство  sin x = √3/2,  уже найдены выше. Поэтому рассмотрим лишь решение Итак, наибольшее значение достигается либо в точке x = π/2, либо на границах отрезка, т.е. в точках x = 0 или x = π. Вычисления приводят к следующим результатам: Таким образом, наибольшее значение равно  √3/2 ≈ 1.732  и оно достигается в двух точках: x = 0, x = π.