|
Дифференцирование и интегрирование рядов Фурье
|
||||||||||||
|
Дифференцирование рядов Фурье
Пусть 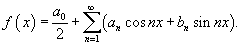 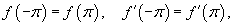 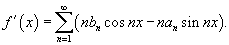
Интегрирование рядов Фурье
Пусть Разложение функции 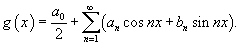 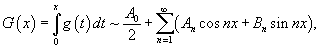 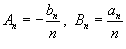 . .Полагая 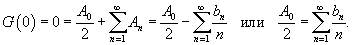 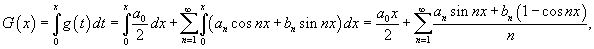 В последнем выражении из-за интегрирования постоянной величины возникло "лишнее" слагаемое, зависящее от x. Поэтому, чтобы сохранить определенную симметрию с разложением в ряд Фурье исходной функции 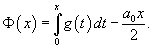 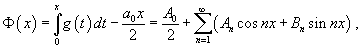 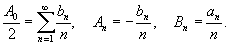 |
||||||||||||
|
Пример 1
|
||||||||||||
|
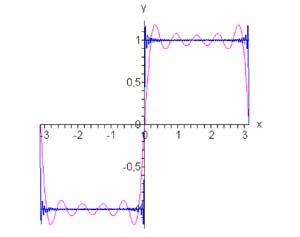
Найти ряд Фурье для функции
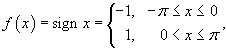 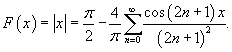 Решение. 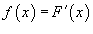 для всех для всех 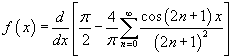 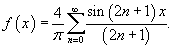
|
||||||||||||
|
Пример 2
|
||||||||||||
|
Найти ряд Фурье функции
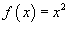 , зная, что , зная, что
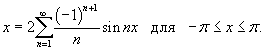 Решение. 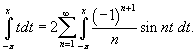 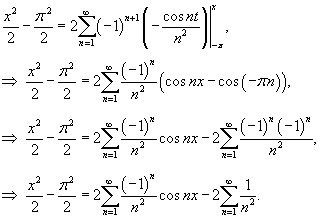 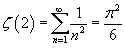 . Отсюда находим, что . Отсюда находим, что
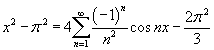 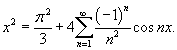 |
||||||||||||
|
Пример 3
|
||||||||||||
|
Найти ряд Фурье функции
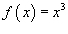 , если известно, что , если известно, что
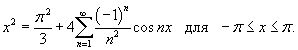 Решение. 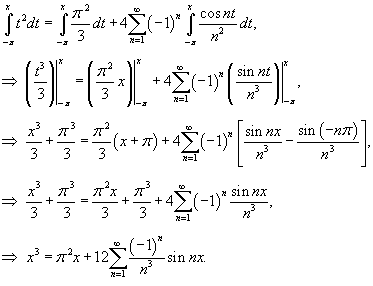 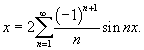 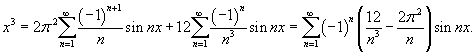 |
||||||||||||
|
Пример 4
|
||||||||||||
|
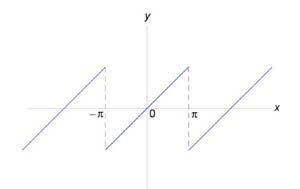
Исследовать процесс почленного дифференцирования ряда Фурье функции
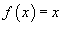 , заданной на интервале , заданной на интервале Решение. 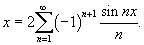 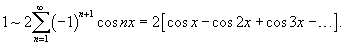 Чтобы объяснить этот парадокс, введем дельта-функцию Дирака 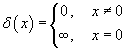 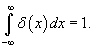 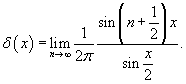
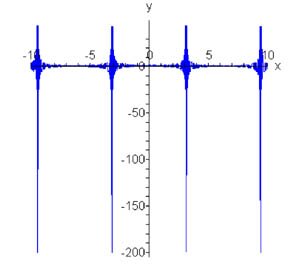
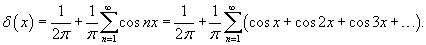 Рассмотрим теперь периодическое продолжение 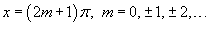 . Соответствующая производная . Соответствующая производная 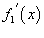 содержит дельта-функцию в каждой точке разрыва, так что справедливо соотношение содержит дельта-функцию в каждой точке разрыва, так что справедливо соотношение
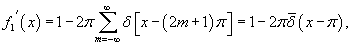 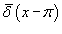 обозначает 2π-периодическое продолжение дельта-функции. обозначает 2π-периодическое продолжение дельта-функции.Отсюда видно, что 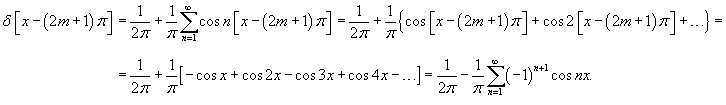 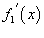 в ряд имеет вид в ряд имеет вид
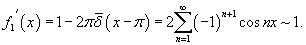 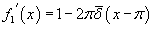 представляет собой ряд Фурье для числа 1. График этой функции приведен ниже на рисунке 4. представляет собой ряд Фурье для числа 1. График этой функции приведен ниже на рисунке 4.
|
||||||||||||