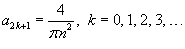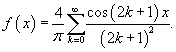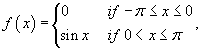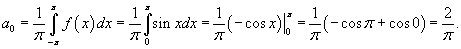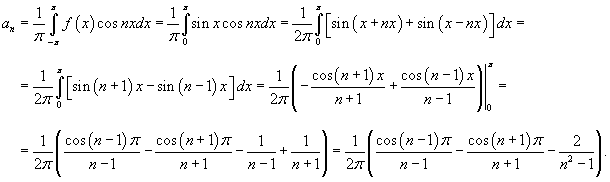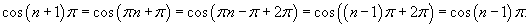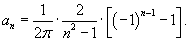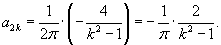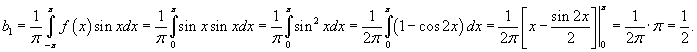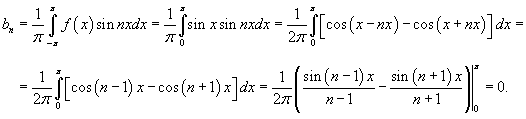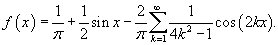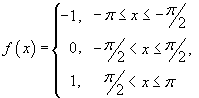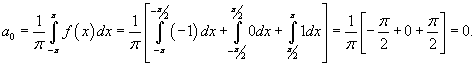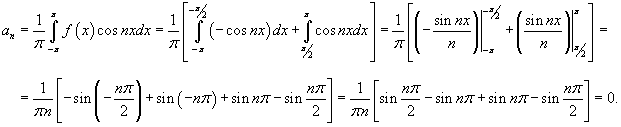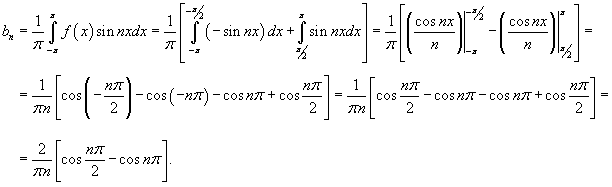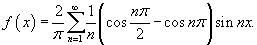|
|
|
|
Определение ряда Фурье и типичные примеры
|
|
|
|
|
Идея о том, что любая периодическая функция может быть представлена в виде ряда гармонически связанных синусов и косинусов была предложена бароном Жан Батистом Жозефом Фурье (1768 − 1830).
Чтобы рассмотреть эту идею более детально, введем базовые определения.
|
Определение ряда Фурье
Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функции f (x) равен 2 π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].
- Предположим, что функция f (x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:
- Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).
Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье).
Если x0 − точка разрыва, то ряд Фурье сходится к значению
Ряд Фурье функции f (x) представляется в виде
где коэффициенты Фурье a0, an и bn определяются формулами
Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя an и bn новыми переменными dn и φn или dn и θn , где
можно, соответственно, записать
Разложение в ряд Фурье четных и нечетных функций
Разложение в ряд Фурье четной функции f (x) с периодом 2 π не содержит синусов и имеет вид
где коэффициенты Фурье определяются выражениями
Аналогично, разложение в ряд Фурье нечетной функции f (x), имеющей период 2 π содержит только синусы и имеет вид
где ы bn равны
Ниже мы рассмотрим некоторые типичные примеры разложения функций с периодом 2 π в ряд Фурье, предполагая, что такие разложения существуют и сходятся к заданной функции.
|
|
Пример 1
|
|
Пусть функция f (x) имеет период 2 π и раскладывается в ряд Фурье:
Вычислить коэффициенты a0, an и bn.
Решение.
Чтобы найти an, проинтегрируем ряд Фурье в интервале [−π, π]:
Для всех n > 0 справедливо
Поэтому, все члены в разложении Фурье справа от знака суммы равны нулю, что приводит к соотношению
Чтобы определить коэффициенты an при m > 0, умножим обе части разложения в ряд Фурье на cos mx и проинтегрируем почленно:
Первое слагаемое в правой части равно нулю. Тогда, используя тригонометрические тождества, можно записать
если m ≠ n.
В случае, если m = n, получаем
Таким образом,
Аналогично, умножая ряд Фурье на sin mx и интегрируя почленно, получим выражение для bm:
Переписывая формулы для an, bn, запишем окончательные выражения для коэффициентов Фурье:
|
|
Пример 2
|
|
Найти разложение в ряд Фурье прямоугольной функции с периодом 2 π, определенной в интервале [−π, π]:
Решение.
Вычислим сначала a0:
Определим теперь коэффициенты Фурье при n ≠ 0:
Поскольку 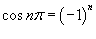 , то можно записать
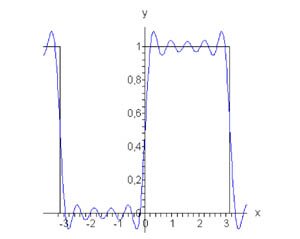
Таким образом, разложение в ряд Фурье для прямоугольной функции имеет вид
Можно легко вычислить несколько первых членов разложения. Полагая, например, n = 5, получаем
На рисунке 1 представлены график данной функции и ее аппроксимация рядом Фурье при n = 10.
|
|
|
|
|
Рис.1, n = 10
|
|
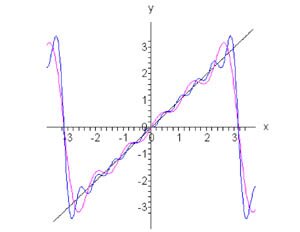
Рис.2, n = 5, n = 10
|
|
|
Пример 3
|
|
Найти разложение в ряд Фурье для пилообразной функции, определенной в интервале [−π, π] и имеющей период 2 π.
Решение.
Определим коэффициенты Фурье для пилообразной волны.
Поскольку функция нечетная (рисунок 2), то a0 = an = 0.
Для вычисления последнего интеграла используем формулу интегрирования по частям:
Пусть 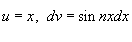 . Тогда 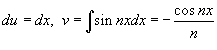 , и интеграл будет равен
Подставляя 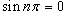 и 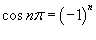 для всех натуральных значений n, получаем
Следовательно, разложение в ряд Фурье прилообразной волны имеет вид (рисунок 2 выше)
|
|
Пример 4
|
|
Предположим, что f (x) является периодической функцией с периодом 2 π. Пусть 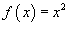 для 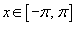 . Найти разложение Фурье для заданной параболической функции.
Решение.
Так как функция четная, то коэффициенты bn = 0. Тогда
Применим дважды интегрирование по частям.
Поскольку 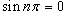 и 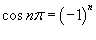 для натуральных n, то получаем
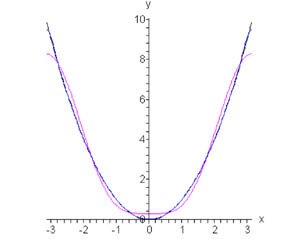
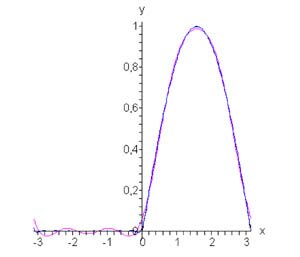
Тогда разложение параболической функции в ряд Фурье имеет вид (рисунок 3)
|
|
|
|
|
Рис.3, n = 2, n = 5
|
|
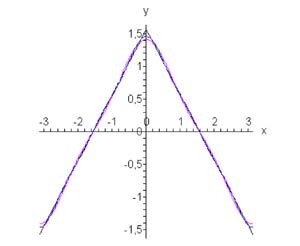
Рис.4, n = 1, n = 2
|
|
|
Пример 5
|
|
Найти ряд Фурье для треугольной волны
определенной в интервале [−π, π].
Решение.
Постоянная a0 равна
Вычислим коэффициенты an:
Интегрируя по частям, можно записать
Тогда
Значения sin nx при x = 0 или x = ± π равны нулю. Поэтому
Если n = 2k, то 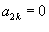 . Если n = 2k + 1, то 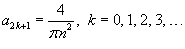
Так как функция f (x) четная, то коэффициенты Фурье bn равны нулю. Таким образом, окончательное разложение треугольной волны в ряд Фурье выглядит следующим образом (см. рис.4 выше):
|
|
Пример 6
|
|
Найти разложение в ряд Фурье для функции
заданной в интервале [−π, π].
Решение.
Найдем сначала a0:
Далее вычислим коэффициенты an:
Заметим, что
Поскольку cos (n − 1)π = (−1)n −1, то для коэффициентов an получаем выражение
Видно, что an = 0 для нечетных n. Для четных n, когда n = 2k (k = 1,2,3,...), мы имеем
Вычислим теперь коэффициенты bn. Начнем с b1:
Остальные коэффициенты bn при n > 1 равны нулю. Действительно,
Таким образом, формула разложения заданной функции в ряд Фурье имеет вид
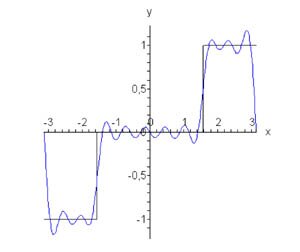
График функции и варианты разложения для n = 2 и n = 8 показаны на рисунке 5.
|
|
|
|
|
Рис.5, n = 2, n = 8
|
|
Рис.6, n = 10
|
|
|
Пример 7
|
|
Найти ряд Фурье для функции
определенной в интервале [−π, π].
Решение.
Вычислим коэффициенты an:
(Этот результат очевиден, поскольку заданная функция − нечетная.)
Определим коэффициенты разложения bn:
Таким образом, разложение в ряд Фурье определяется формулой
На рисунке 6 (выше) представлен график исходной прямоугольной функции и ее Фурье аппроксимации при n = 10.
|
|
|
|



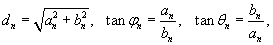
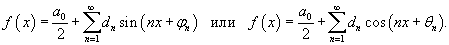
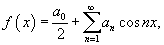
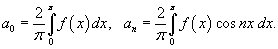
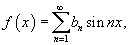
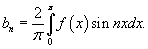
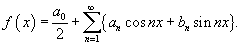
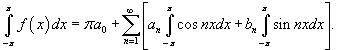
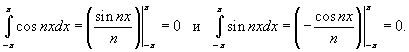
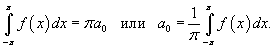
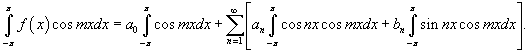
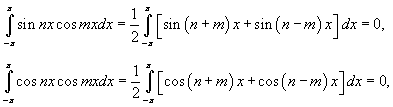
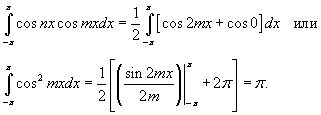
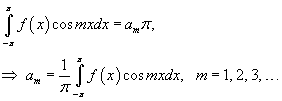
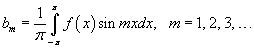
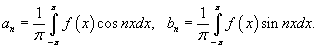
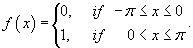
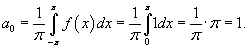
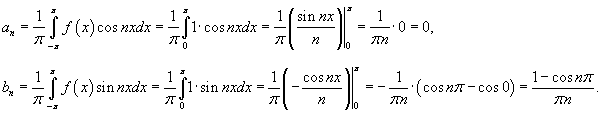
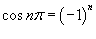 , то можно записать
, то можно записать
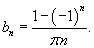
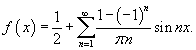
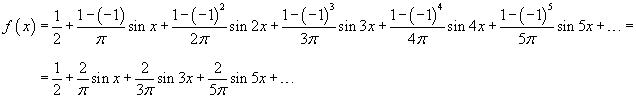
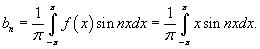
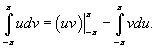
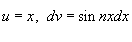 . Тогда
. Тогда 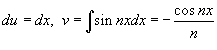 , и интеграл будет равен
, и интеграл будет равен
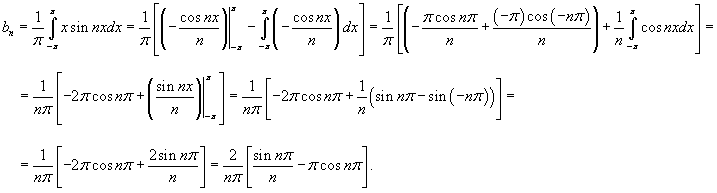
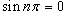 и
и 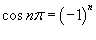 для всех натуральных значений n, получаем
для всех натуральных значений n, получаем
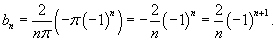
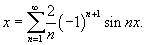
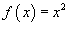 для
для 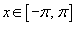 . Найти разложение Фурье для заданной параболической функции.
. Найти разложение Фурье для заданной параболической функции.
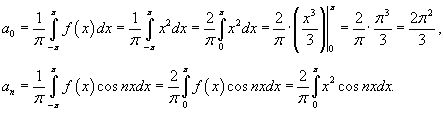
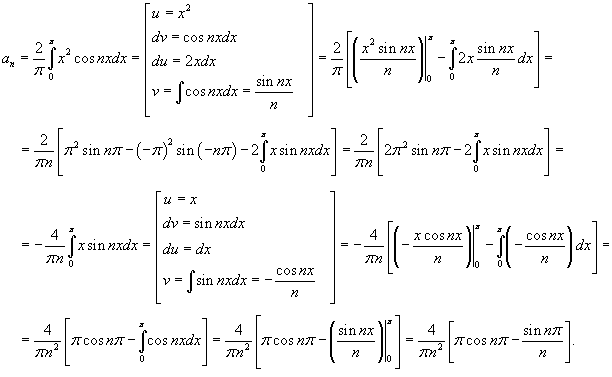
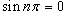 и
и 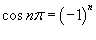 для натуральных n, то получаем
для натуральных n, то получаем
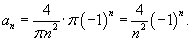
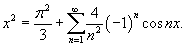
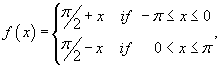
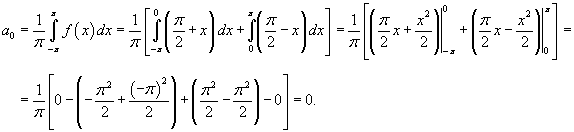
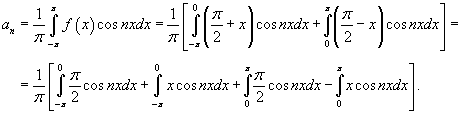
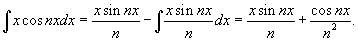
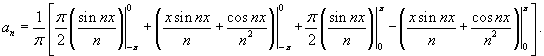
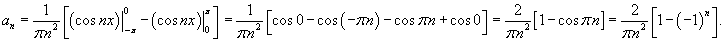
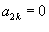 . Если
. Если