|
Неравенство Бесселя и равенство Парсеваля
|
|
Неравенство Бесселя
Рассмотрим кусочно непрерывную функцию 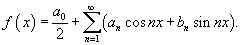 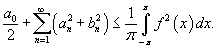 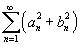 сходится. сходится.
Равенство Парсеваля
Если 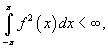 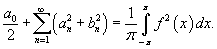
Формула Парсеваля в комплексной форме
Снова предположим, что 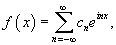 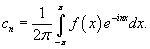 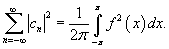 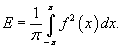 |
|
Пример 1
|
|
Вычислить сумму ряда
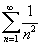 . Указание: применить формулу Парсеваля к функции . Указание: применить формулу Парсеваля к функции Решение. 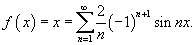 Здесь коэффициенты Фурье имеют следующие значения: 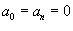 (поскольку функция (поскольку функция  . Используя формулу Парсеваля. получаем . Используя формулу Парсеваля. получаем
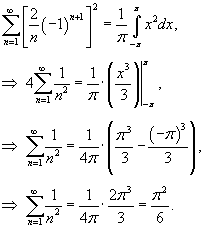 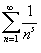 называется дзета-функцией Римана называется дзета-функцией Римана 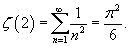 . . |
|
Пример 2
|
|
Применить формулу Парсеваля к функции
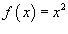 . .
Решение. 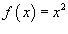 в ряд Фурье в интервале в ряд Фурье в интервале 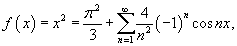 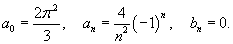 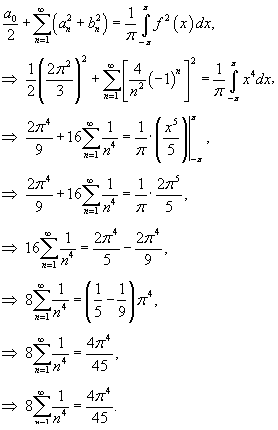 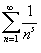 известен как дзета-функция Римана известен как дзета-функция Римана 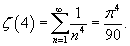 |
|
Пример 3
|
|
Применяя формулу Парсеваля к функции
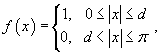 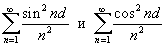 . .
Решение. 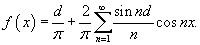 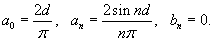 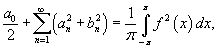 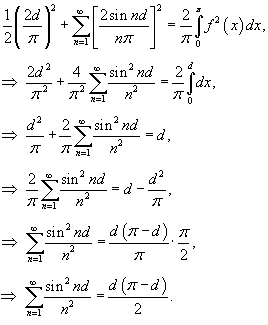 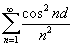 : :
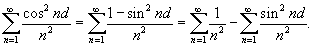 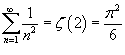 (смотрите пример 1 выше). Следовательно, (смотрите пример 1 выше). Следовательно,
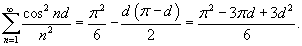 |
|
Пример 4
|
|
Вычислить сумму ряда
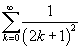 . .
Решение. 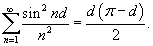 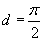 , получаем , получаем
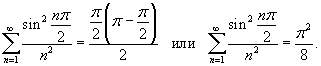 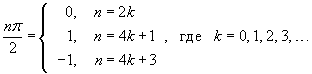 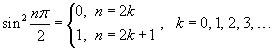 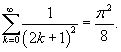 |