|
Производная показательной и логарифмической функций
|
|
На странице Определение производной мы вывели формулы производной экспоненциальной функции y = e x и функции натурального логарифма y = ln x. Ниже мы рассмотрим показательную и логарифмическую функцию с произвольным основанием и получим выражения для их производных.
Производная логарифмической функции
Начнем с производной логарифмической функции y = loga x, где основание a больше нуля и не равно единице: a > 0, a ≠ 1. Согласно определению производной, дадим аргументу x приращение Δx > 0, причем предположим, что x + Δx > 0. Логарифмическая функция получит соответствующее приращение Δy, равное
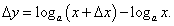 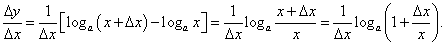 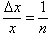 . Тогда последнее соотношение можно переписать в виде . Тогда последнее соотношение можно переписать в виде
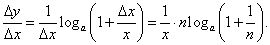 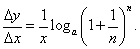 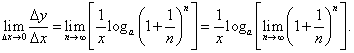 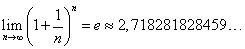 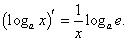 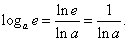 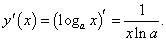 Отметим еще один важный частный случай − производную десятичного логарифма: 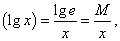
Производная показательной функции
Поскольку показательная функция с основанием a (a > 0, a ≠ 1) и логарифмическая функция с тем же основанием образуют пару взаимно-обратных функций, то производную показательной функции можно найти с помощью теоремы о производной обратной функции.Пусть дана пара взаимно-обратных функций y = f (x) = a x и x = φ(y) = loga y. Тогда 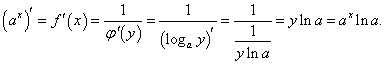 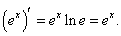 |
|
Пример 1
|
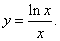
Решение.
Дифференцируем как частное двух функций:
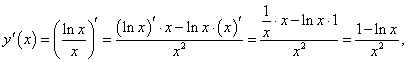 |
|
Пример 2
|
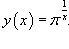
Решение.
Дифференцируя данную показательную функцию как сложную, находим
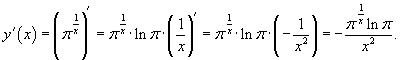 |
|
Пример 3
|
|
y = x ln x − x.
Решение.
Используя правила дифференцирования произведения функций и разности функций, получаем:
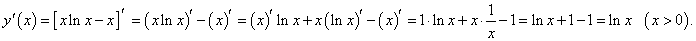 |
|
Пример 4
|
|
y = log2 cos x.
Решение.
Дифференцируя как сложную функцию, имеем
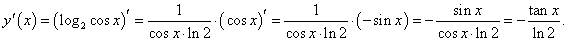 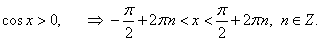 |
|
Пример 5
|
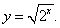
Решение.
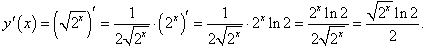 |
|
Пример 6
|
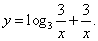
Решение.
Применяя линейные свойства производной и правило дифференцирования сложной функции, получаем
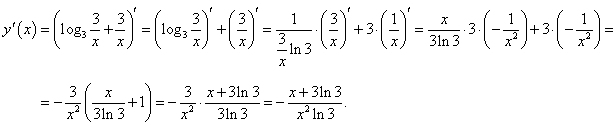 |
|
Пример 7
|
|
y = log3 (4x2).
Решение.
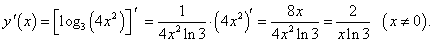 |
|
Пример 8
|

Решение.
По правилу дифференцирования сложной функции находим
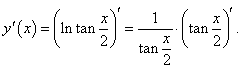 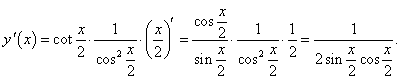 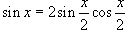 , получаем окончательный ответ , получаем окончательный ответ
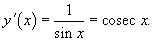 |
|
Пример 9
|
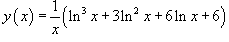
Решение.
Сначала возьмем производную от произведения функций:
 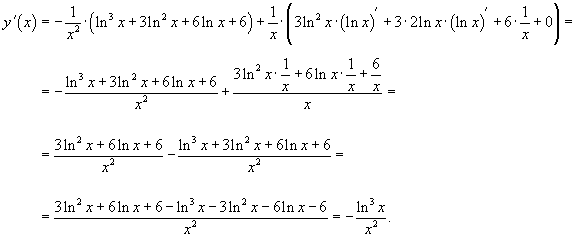 |
|
Пример 10
|
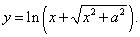
Решение.
Дифференцируя как сложную функцию и упрощая, получаем следующее выражение для производной:
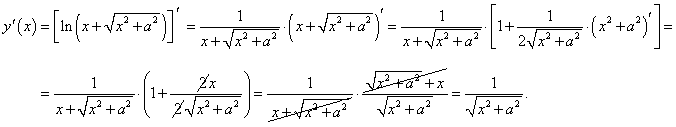 |
|
Пример 11
|
|
y = 4x⋅32x.
Решение.
Используя правила дифференцирования произведения двух функций и сложной функции, получаем:
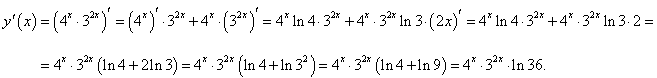 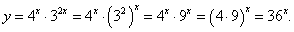 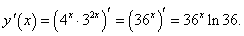 |
|
Пример 12
|
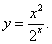
Решение.
По формуле производной частного двух функций находим:
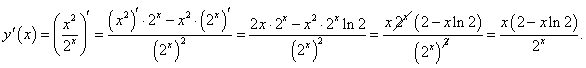 |
|
Пример 13
|
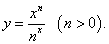
Решение.
Здесь в числителе и знаменателе находятся, соответственно, степенная и показательная функции. Используя правило дифференцирования частного, получаем:
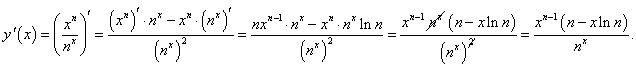 |
|
Пример 14
|
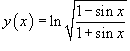
Решение.
Используем формулы производной сложной функции и производной частного. После небольших преобразований получаем вполне "приличный" ответ.
 |
|
Пример 15
|
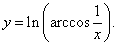
Решение.
Дважды применяем правило дифференцирования сложной функции:
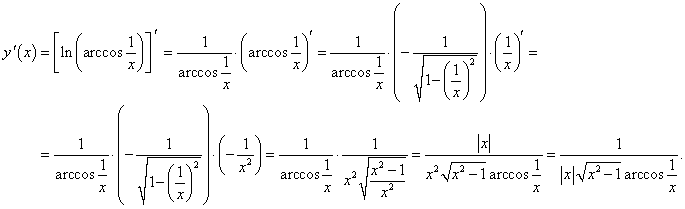 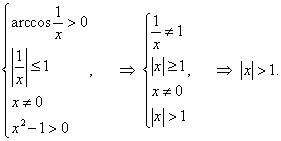 |
|
Пример 16
|
|
y = ln (ln cot x).
Решение.
Дифференцируя дважды как сложную функцию, получаем
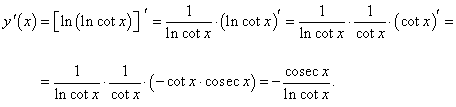 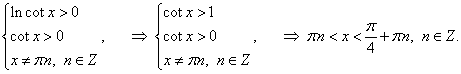 |
|
Пример 17
|
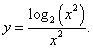
Решение.
По формуле производной частного находим:
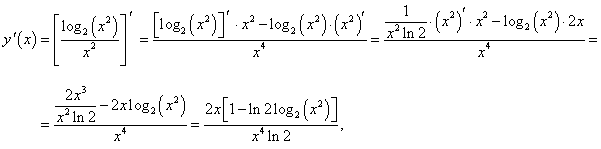 |
|
Пример 18
|
|
Показать, что функция y = e x(sin 2x + cos 2x) является решением дифференциального уравнения
y'' −2y' + 5y = 0.
Решение.
Вычислим производные y' и y'':
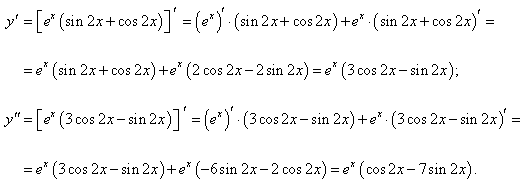 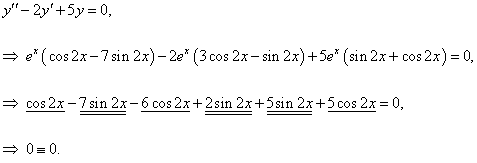 |
|
Пример 19
|
|
Показать, что функция y = e−2x(sin 3x + cos 3x) является решением дифференциального уравнения
y'' + 4y' + 13y = 0.
Решение.
Найдем первую и вторую производные заданной функции:
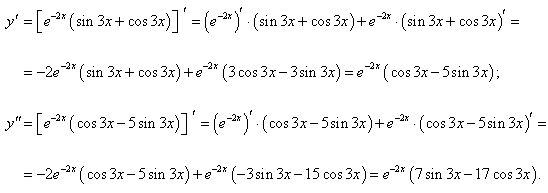 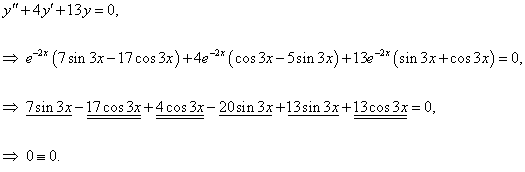 |
|
Пример 20
|
|
y = ln (tan x + sec x).
Решение.
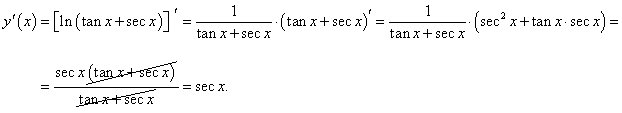 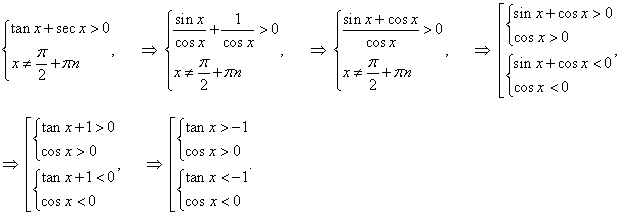 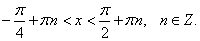 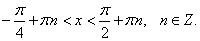 |