|
Число е
|
|
Число e выражается через предел следующим образом:
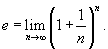 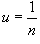 , где , где 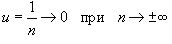 , получим альтернативную формулу для данного предела: , получим альтернативную формулу для данного предела:
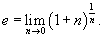 |
|
Пример 1
|
|
Вычислить предел
 . .
Решение. 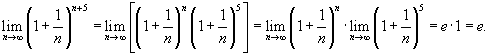 |
|
Пример 2
|
|
Вычислить предел
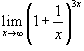 . .
Решение. 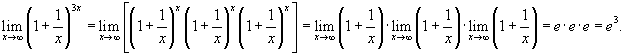 |
|
Пример 3
|
|
Вычислить предел
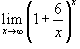 . .
Решение. 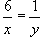 , так что , так что 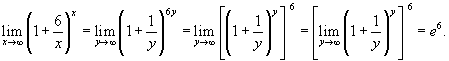 |
|
Пример 4
|
|
Вычислить предел
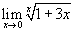 . .
Решение. 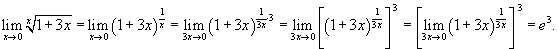 |
|
Пример 5
|
|
Вычислить предел
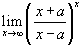 . .
Решение. 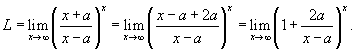 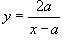 . Если . Если 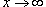 , то , то 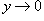 и и
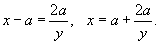 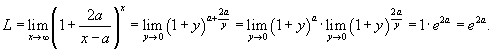 |
|
Пример 6
|
|
Вычислить предел
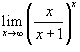 . .
Решение. 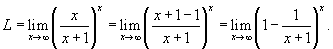 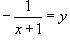 . Тогда . Тогда
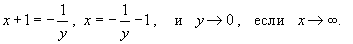  |
|
Пример 7
|
|
Вычислить предел
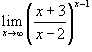 . .
Решение. 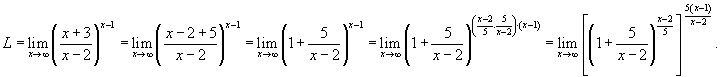 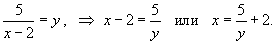 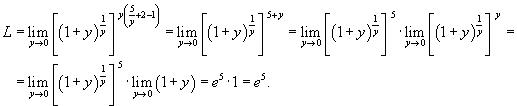 |
|
Пример 8
|
|
Найти предел
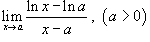 . .
Решение. 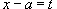 . Легко видеть, что . Легко видеть, что 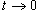 при при 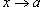 . Тогда . Тогда
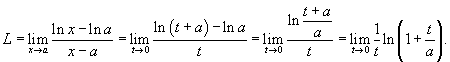 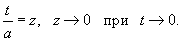 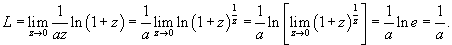 |
|
Пример 9
|
|
Найти предел
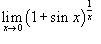 . .
Решение. 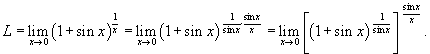 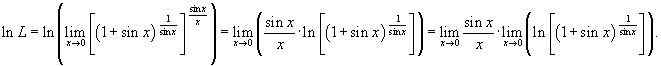 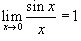 . Кроме того, . Кроме того, 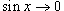 при при 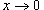 , поэтому предельный переход , поэтому предельный переход 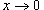 во втором пределе можно заменить на во втором пределе можно заменить на 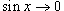 . Это приводит к следующему выражению: . Это приводит к следующему выражению:
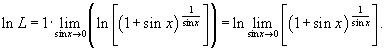 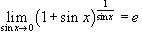 , получаем , получаем
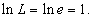 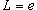 . . |
|
Пример 10
|
|
Найти предел
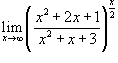 . .
Решение. 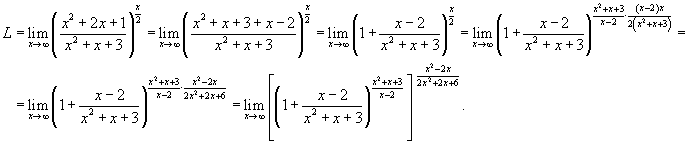 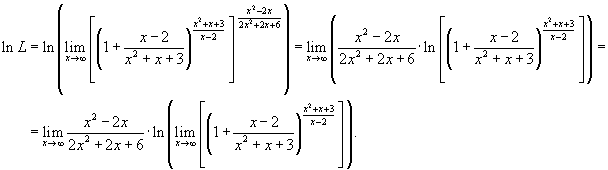 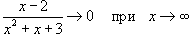 . Тогда второй предел равен e. В результате получаем . Тогда второй предел равен e. В результате получаем
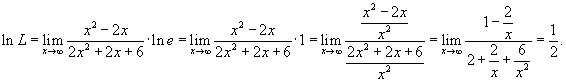 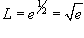 . .
|