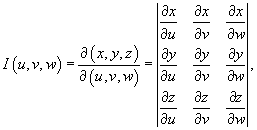|
Замена переменных в тройных интегралах
|
|
При вычислении тройного интеграла, как и двойного, часто удобно сделать замену переменных. Это позволяет упростить вид области интегрирования или подынтегральное выражение.
Пусть исходный тройной интеграл задан в декартовых координатах 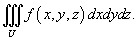 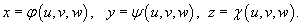
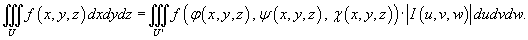 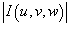 означает абсолютное значение якобиана. означает абсолютное значение якобиана.Для вычисления тройных интегралов часто используются цилиндрические и сферические координаты. Эти случаи рассматриваются подробно на страницах Ниже приводятся примеры вычисления интегралов с использованием других преобразований координат. |
|
Пример 1
|
|
Найти объем области U, заданной неравенствами
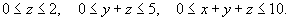 Решение. Сделаем следующую замену: 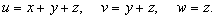 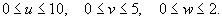 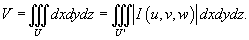 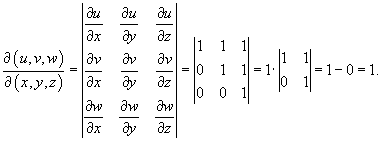 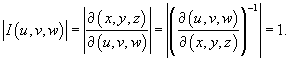 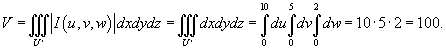 |
|
Пример 2
|
|
Найти объем наклонного параллелепипеда, заданного неравенствами
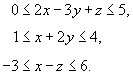 Решение. 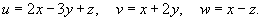 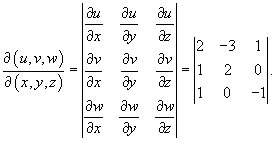 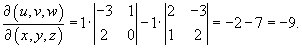 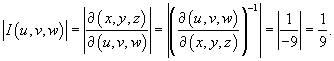 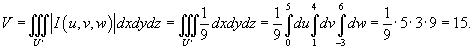 |