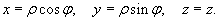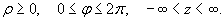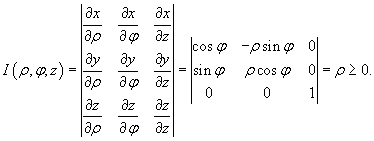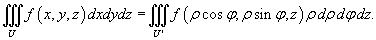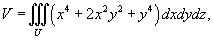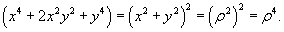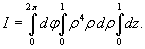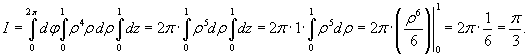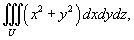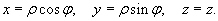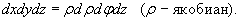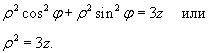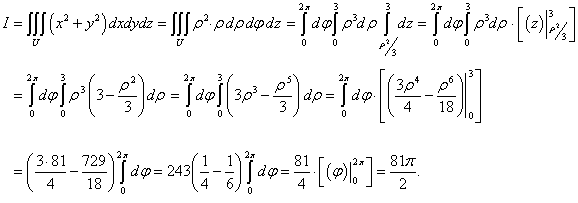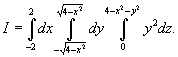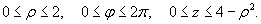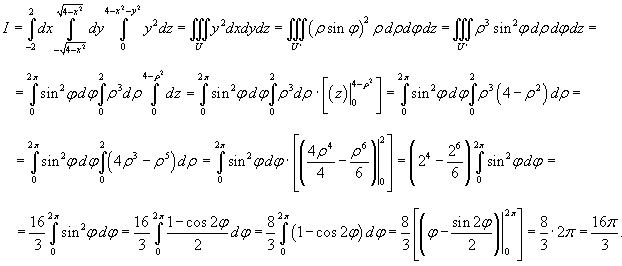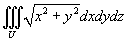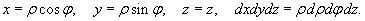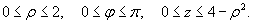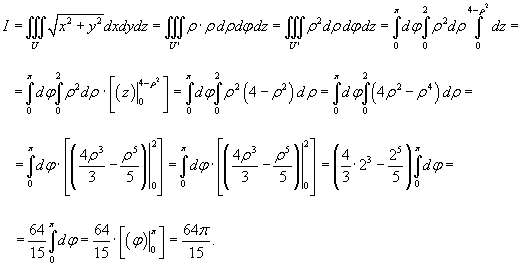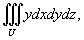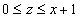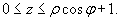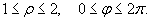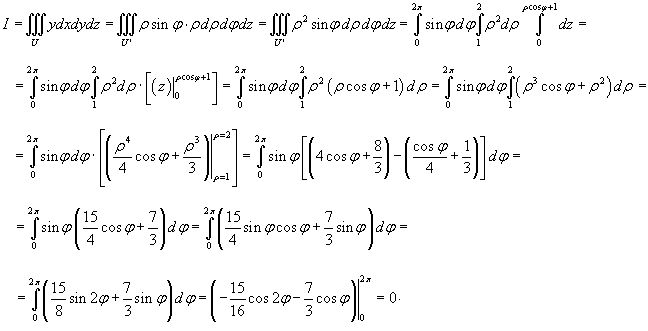Тройные интегралы в цилиндрических координатах

В цилиндрических координатах положение точки M(x,y,z) в пространстве Oxyz определяется тремя числами − ρ, φ, z , где ρ − длина радиуса-вектора проекции точки M на плоскость Oxy, φ − угол, образованный этим радиусом-вектором с осью Ox (рисунок 1), z − проекция на ось Oz (ее значение одинаково в декартовых и цилиндрических координатах). Цилиндрические координаты точки связаны с ее декартовыми координатами соотношениями Здесь предполагается, что Якобиан перехода от декартовых координат к цилиндрическим равен Тогда формула замены переменных при данном преобразовании имеет вид: Переход к цилиндрическим координатам упрощает вычисление тройного интеграла в случаях, когда область интегрирования образована цилиндрической поверхностью.

   Пример 1

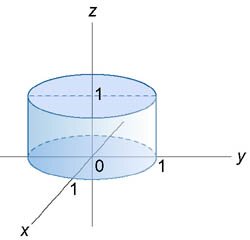
Вычислить интеграл где область U ограничена поверхностью x² + y² ≤ 1 и плоскостями z = 0, z = 1 (рисунок 2). Данный интеграл удобно вычислить в цилиндрических координатах. Проекция области интегрирования на плоскость Oxy представляет собой круг x² + y² ≤ 1 или 0 ≤ ρ ≤ 1 (рисунок 3).

Заметим, что подынтегральное выражение записывается в виде Тогда интеграл будет равен Здесь во втором интеграле добавлен множитель ρ − якобиан преобразования декартовых координат в цилиндрические. Все три интеграла по каждой из переменной не зависят друг от друга. В результате тройной интеграл легко вычисляется:

   Пример 2

Вычислить интеграл где область U ограничена поверхностями x² + y² = 3z, z = 3 (рисунок 4). Область интегрирования изображена на рисунке 4. Для вычисления интеграла перейдем к цилиндрическим координатам: Дифференциал при этом равен Уравнение параболической поверхности принимает вид: Проекция области интегрирования U на плоскость Oxy представляет собой окружность x² + y² ≤ 9 радиусом ρ = 3 (рисунок 5). Координата ρ изменяется в пределах от 0 до 3, угол φ − от 0 до 2π, и координата z − от ρ²/3 до 3. В результате интеграл будет равен

   Пример 3

Используя цилиндрические координаты, найти значение интеграла Область интегрирования U изображена на рисунке 6. Ее проекция на плоскость Oxy представляет собой круг x² + y² = 2² (рисунок 7).

Новые переменные в цилиндрических координатах будут изменяться в пределах Подставляя x = ρ cos φ и y = ρ sin φ, найдем значение интеграла:

   Пример 4

Вычислить интеграл, используя цилиндрические координаты: Область U ограничена параболоидом  z = 4 − x² − y², цилиндром x² + y² = 4 и плоскостями y = 0, z = 0 (рисунок 8). Изобразив схематически область интегрирования U, находим, что ее проекция на плоскость Oxy (область D) представляет собой полукруг радиусом ρ = 2 (рисунок 9).

Перейдем к цилиндрическим координатам, применяя подстановки Новые переменные будут изменяться в пределах Теперь вычисляем интеграл:

   Пример 5

Найти интеграл где область U ограничена плоскостями z = x + 1, z = 0 и цилиндрическими поверхностями x² + y² = 1, x² + y² = 4 (рисунок 10). Вычислим данный интеграл в цилиндрических координатах. Из условия следует, что Область интегрирования в плоскости Oxy представляет собой кольцо, ограниченное окружностями x² + y² = 1 и x² + y² = 4 (рисунок 11). Следовательно, переменные ρ и φ изменяются в интервале Находим интеграл: Этот результат закономерен, поскольку область U симметрична относительно плоскости Oxz, а подынтегральная функция является четной.