|
Тройные интегралы в сферических координатах
|
||||||
|
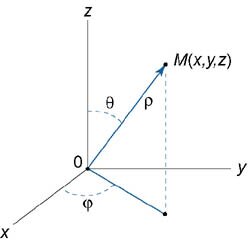
Сферическими координатами точки
ρ − длина радиуса-вектора точки M;
φ − угол, образованный проекцией радиуса-вектора 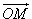 на плоскость Oxy и осью Ox; на плоскость Oxy и осью Ox;θ − угол отклонения радиуса-вектора 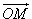 от положительного направления оси Oz (рисунок 1). от положительного направления оси Oz (рисунок 1).
Сферические координаты точки связаны с ее декартовыми координатами соотношениями      Иногда выгодно использовать т.н. обощенные сферические координаты, связанные с декартовыми формулами 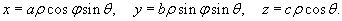 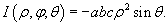 |
||||||
|
Пример 1
|
||||||
|
Найти интеграл
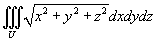 , где область интегрирования U − шар, заданный уравнением , где область интегрирования U − шар, заданный уравнением Решение. 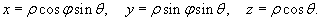 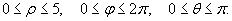 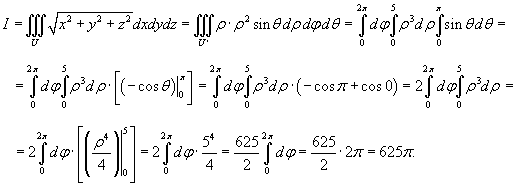 |
||||||
|
Пример 2
|
||||||
|
Вычислить интеграл
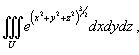 Решение. 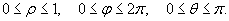 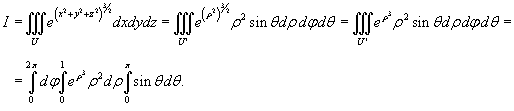 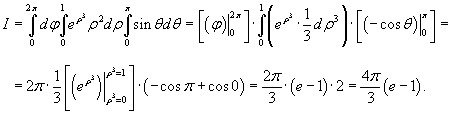 |
||||||
|
Пример 3
|
||||||
|
Вычислить интеграл
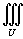 Решение. 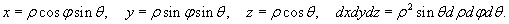 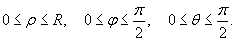 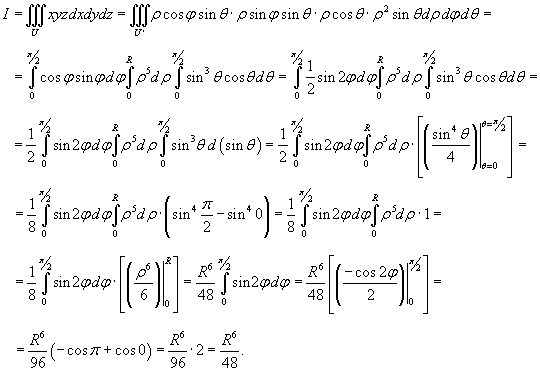 |
||||||
|
Пример 4
|
||||||
|
Найти тройной интеграл
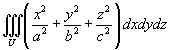 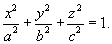 Решение. 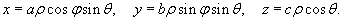  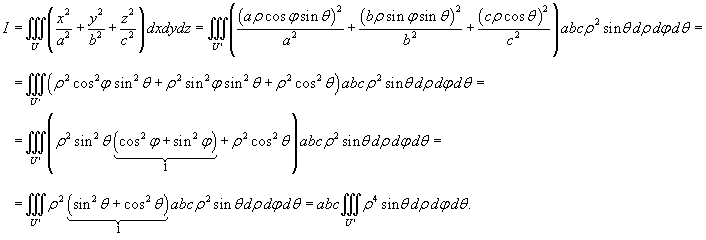 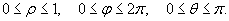 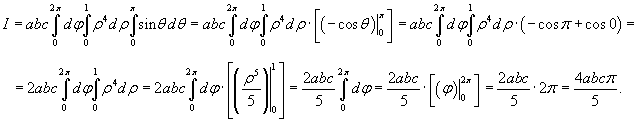 |
||||||
|
Пример 5
|
||||||
|
Вычислить интеграл
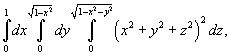 Решение. 
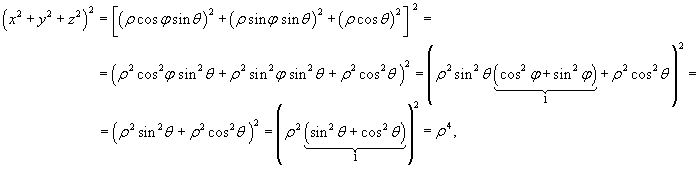 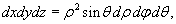 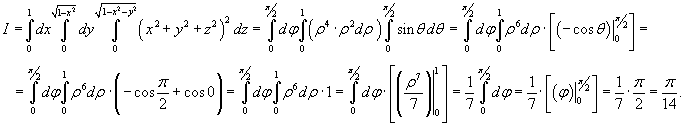 |
||||||