|
Асимптоты
|
||||||||||||
|
Асимптотой кривой y = f(x), имеющей бесконечную ветвь, называется прямая, расстояние которой от точки (x, f(x)), лежащей на кривой, стремится к нулю при неограниченном движении вдоль ветви к бесконечности.
Асимптоты могут быть вертикальными, наклонными и горизонтальными. Горизонтальную асимптоту часто рассматривают как частный случай наклонной асимптоты.
Вертикальная асимптота
Прямая x = a является вертикальной асимптотой графика функции y = f(x), если выполнено хотя бы одно из условий:
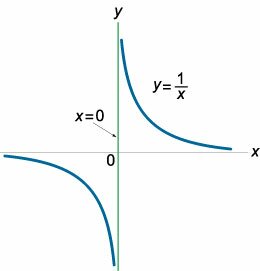
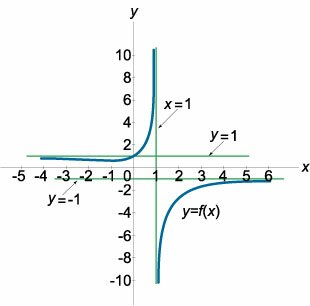
 Вертикальная асимптота часто встречается у дробно-рациональных функций в точках, где знаменатель равен нулю, а числитель не равен нулю (т.е. в точках разрыва второго рода). Например, график функции y = 1/x имеет вертикальную асимптоту x = 0 (рисунок 1). В данном случае оба односторонних предела (слева и справа) стремятся к бесконечности: 
Наклонная асимптота
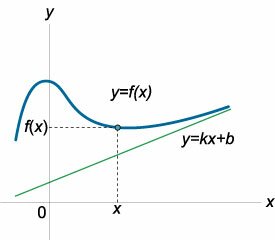
Прямая y = kx + b называется наклонной асимптотой графика функции y = f(x) при x → +∞ (рисунок 2), если
 Наклонные асимптоты графика функции y = f(x) могут быть разными при x → +∞ и x → −∞. Поэтому при нахождении наклонных (или горизонтальных) асимптот оба случая следует рассматривать отдельно. Коэффициенты k и b наклонной асимптоты y = kx + b определяются с помощью следующей теоремы: Для того, чтобы прямая y = kx + b была асимптотой графика функции y = f(x) при x → +∞, необходимо и достаточно, чтобы существовали два конечных предела:  Необходимость. Пусть прямая y = kx + b является асимптотой графика функции y = f(x) при x → +∞. Тогда выполняется условие       Замечание: Аналогично доказывается теорема для случая x → −∞.
Горизонтальная асимптота
В частном случае, если k = 0, мы получаем горизонтальную асимптоту, которая описывается уравнением y = b. Теорема о необходимых и достаточных условиях существования горизонтальной асимптоты формулируется таким образом:Для того, чтобы прямая y = b была асимптотой графика функции y = f(x) при x → +∞, необходимо и достаточно, чтобы существовал конечный предел: 
Асимптоты кривой, заданной параметрически
Пусть плоская кривая задана параметрическими уравнениями
   Параметрически заданная кривая имеет наклонную асимптоту y = kx + b при t → t3, если при этом значении t оба предела равны бесконечности:  
Асимптота кривой в полярных координатах
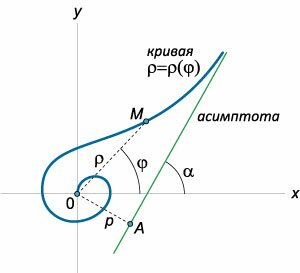
Рассмотрим кривую, заданную в полярных координатах уравнением
 Указанные параметры p и α определяются формулами: 
Асимптоты кривой, заданной неявно
Неявно заданная алгебраическая кривая описывается уравнением
F(x, y) = 0,
где левая часть представляет собой многочлен относительно переменных x и y.В дифференциальной геометрии используется следующий метод нахождения наклонной асимптоты алгебраической кривой. Пусть асимптота описывается уравнением y = kx + b. Подставляя это выражение для y в уравнение кривой, получаем алгебраическое уравнение относительно одной переменной x:     |
||||||||||||
|
Пример 1
|
||||||||||||
|
Найти асимптоты графика функции

Решение.
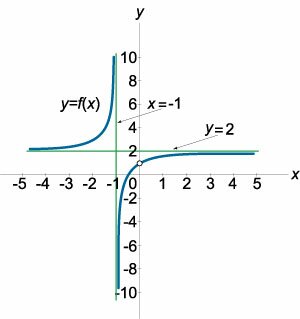
При x = −1 функция имеет разрыв второго рода. Действительно:
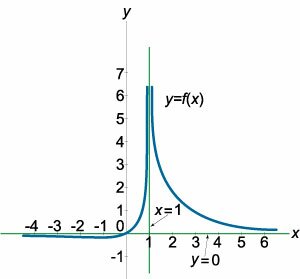
 Найдем горизонтальную асимптоту. Вычислим предел:  Наклонные асимптоты отсутствуют. Это можно проверить, вычислив коэффициенты k и b:  Окончательный ответ: график функции имеет вертикальную асимптоту x = −1 и горизонтальную асимптоту y = 1 (рисунок 4). |
||||||||||||
|
Пример 2
|
||||||||||||
|
Найти асимптоты графика функции

Решение.
Вычислим односторонние пределы в точке x = 1:
 Исследуем наклонные асимптоты:  График функции и его асимптоты приведены на рисунке 5.
|
||||||||||||
|
Пример 3
|
||||||||||||
|
Найти асимптоты графика функции

Решение.
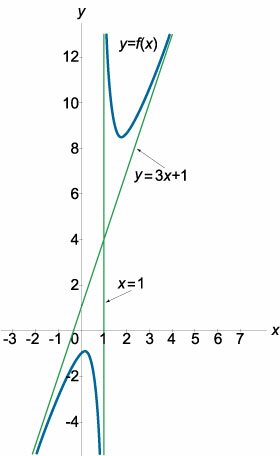
Ясно, что прямая x = 1 является вертикальной асимптотой, поскольку в этой точке функция имеет разрыв и выполняются соотношения
  Таким образом, график функции имеет наклонную асимптоту y = 3x + 1. Заметим, что дробно-рациональная функция может иметь наклонную асимптоту, если степень числителя на единицу больше степени знаменателя. Схематический вид данной кривой приведен выше на рисунке 6. |
||||||||||||
|
Пример 4
|
||||||||||||
|
Найти асимптоты графика функции
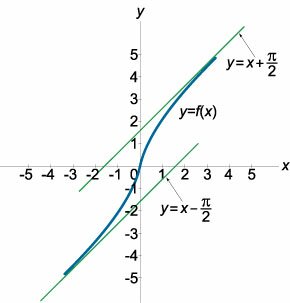
y = x + arctan x.
Решение.
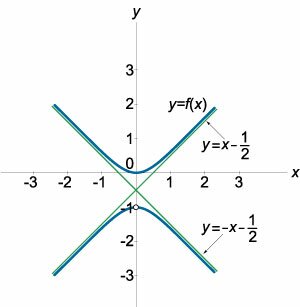
Данная функция непрерывна на всем множестве действительных чисел. Поэтому у нее нет вертикальных асимптот. Исследуем наклонные асимптоты:
  
|
||||||||||||
|
Пример 5
|
||||||||||||
|
Найти асимптоты графика функции

Решение.
Функция имеет разрыв второго рода при x = 1. Так как
 Поскольку порядок роста числителя и знаменателя одинаков, то график имеет также горизонтальную асимптоту. В пределе при x → +∞ получаем   |
||||||||||||
|
Пример 6
|
||||||||||||
|
Найти асимптоты линии, заданной параметрическими уравнениями

Решение.
Исследуем точку t = 2. Вычислим пределы функций x = φ(t) и y = ψ(t) при t → 2:
 Аналогично рассмотрим точку t = 1, в которой терпит разрыв функция y(t):  Из вида функции x = φ(t) следует, что t → 2 − единственное значение параметра t, при котором координата x стремится к бесконечности. Отсюда следует, что кривая не имеет наклонных асимптот. Итак, данная кривая имеет горизонтальную асимптоту y = 2 и вертикальную асимптоту x = −1. Ее схематический вид представлен на рисунке 9.
|
||||||||||||
|
Пример 7
|
||||||||||||
|
Найти асимптоты линии, заданной параметрическими уравнениями

Решение.
При t = ±1 знаменатели в выражениях для x и y равны нулю. Поэтому при этих значениях t имеем:
     Данная линия состоит из двух ветвей, причем нижняя ветвь не определена при x = 0 (когда t → ±∞). Вид кривой показан схематически на рисунке 10. |
||||||||||||
|
Пример 8
|
||||||||||||
|
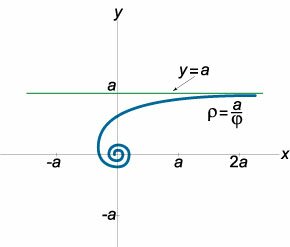
Найти асимптоты гиперболической спирали, заданной уравнением

Решение.
Выразим угол φ через радиус ρ:
   Следовательно, у гиперболической спирали существует горизонтальная асимптота с параметрами α = 0, p = −a. В декартовых координатах ее уравнение имеет вид y = a (рисунок 11).
|
||||||||||||
|
Пример 9
|
||||||||||||
|
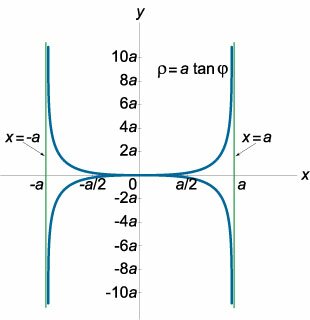
Найти асимптоты кривой, заданной в полярных координатах:
ρ = a tan φ.
Решение.
Выразим из уравнения обратную зависимость φ(ρ):
      |
||||||||||||
|
Пример 10
|
||||||||||||
|
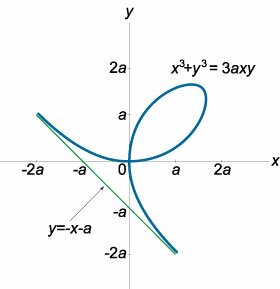
Найти асимптоты декартова листа, заданного уравнением
x3 + y3 = 3axy.
Решение.
Исследуем сначала наклонные асимптоты данной кривой. Запишем неявное уравнение в виде
   Проверим возможность существования вертикальной асимптоты. Пусть ее уравнение записывается как y = с. Подставим это в исходное неявное уравнение кривой: 
|
||||||||||||
|
Пример 11
|
||||||||||||
|
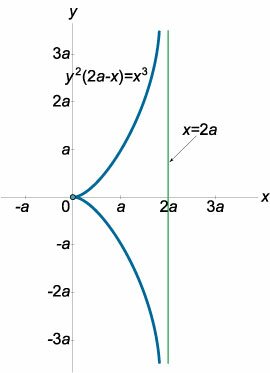
Найти асимптоты циссоиды Диокла, заданной уравнением
y2 (2a − x) = x3, a > 0.
Решение.
Исследуем наклонные асимптоты. Подставим y = kx + b в заданное уравнение:
   Рассмотрим вертикальную асимптоту. Подставляя x = c в исходное уравнение, получаем:   Замечание. Уравнение циссоиды допускает запись в явной форме:  |
||||||||||||
|
Пример 12
|
||||||||||||
|
Доказать, что функции
 Решение.      |
||||||||||||