|
Точки разрыва функции
|
|||||||||||||||
|
Если функция
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.Говорят, что функция
|
|||||||||||||||
|
Пример 1
|
|||||||||||||||
|
Исследовать функцию
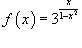 на непрерывность. на непрерывность.
Решение. 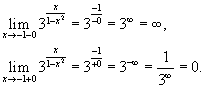  |
|||||||||||||||
|
Пример 2
|
|||||||||||||||
|
Показать, что функция
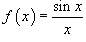 имеет устранимый разрыв в точке имеет устранимый разрыв в точке Решение. 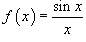 также непрерывна при всех x за исключением точки также непрерывна при всех x за исключением точки Так как 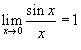 , то в данной точке существует устранимый разрыв. Мы можем сконструировать новую функцию , то в данной точке существует устранимый разрыв. Мы можем сконструировать новую функцию
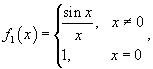 |
|||||||||||||||
|
Пример 3
|
|||||||||||||||
|
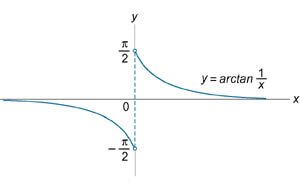
Найти точки разрыва функции
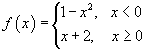 , если они существуют. , если они существуют.
Решение. Вычислим односторонние пределеы при 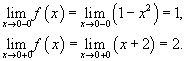 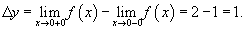 |
|||||||||||||||
|
Пример 4
|
|||||||||||||||
|
Найти точки разрыва функции
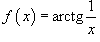 , если они существуют. , если они существуют.
Решение. 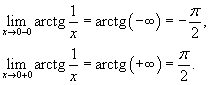
|
|||||||||||||||
|
Пример 5
|
|||||||||||||||
|
Найти точки разрыва функции
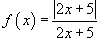 , если таковые существуют. , если таковые существуют.
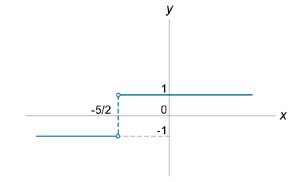
Решение. 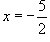 , где существует разрыв. Исследуем точку разрыва. , где существует разрыв. Исследуем точку разрыва.
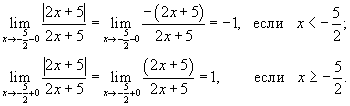 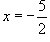 существует разрыв первого рода. График функции схематически показан на рисунке 3. существует разрыв первого рода. График функции схематически показан на рисунке 3.
|
|||||||||||||||




 и правосторонний предел
и правосторонний предел  ;
;

 называется
называется