|
Тройные интегралы в декартовых координатах
|
||||||
|
Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов.
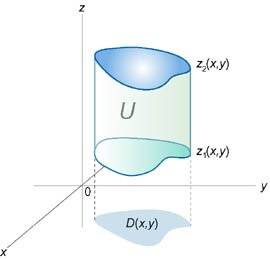
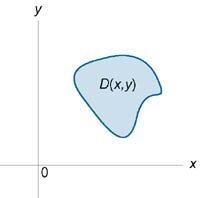
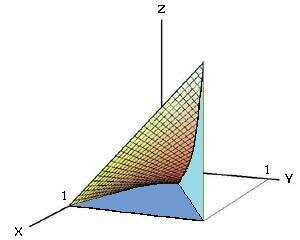
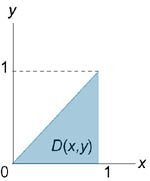
Рассмотрим случай, когда область интегрирования U является элементарной относительно оси Oz, т.е. любая прямая, параллельная оси Oz, пересекает границу области U не более, чем в двух точках. Пусть область U ограничена снизу поверхностью
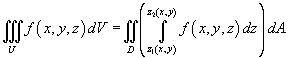 Если область 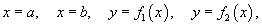 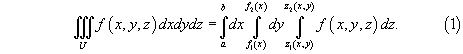 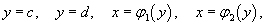 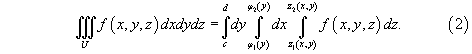 В частном случае, когда область интегрирования U представляет собой прямоугольный параллелепипед 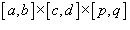 , тройной интеграл вычисляется по формуле , тройной интеграл вычисляется по формуле
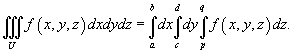 |
||||||
|
Пример 1
|
||||||
|
Вычислить интеграл
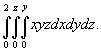 Решение. 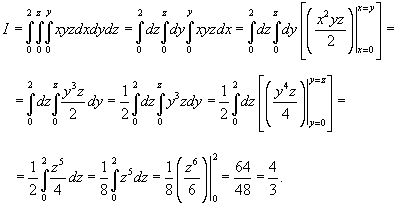 |
||||||
|
Пример 2
|
||||||
|
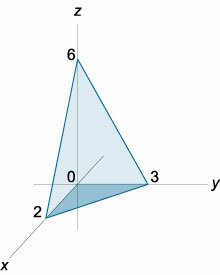
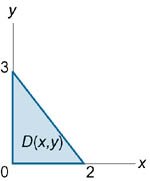
Вычислить интеграл
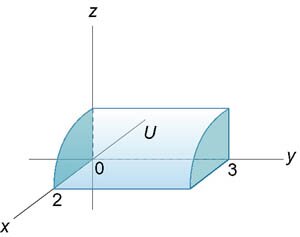
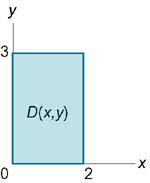
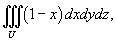 Решение. 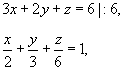
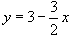 (рисунок 4). При этом переменная x "пробегает" от 0 до 2. (рисунок 4). При этом переменная x "пробегает" от 0 до 2.Итак, тройной интеграл выражается через повторный в виде 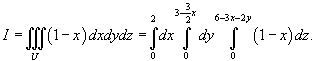 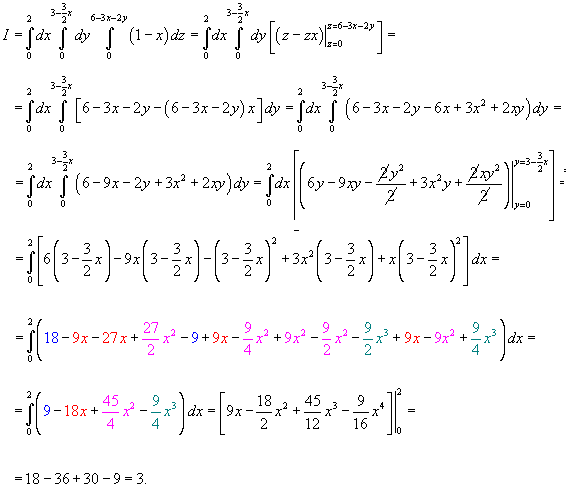 |
||||||
|
Пример 3
|
||||||
|
Вычислить тройной интеграл
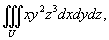 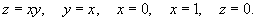
Решение. 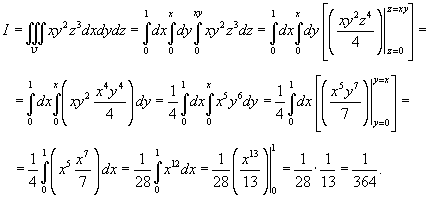 |
||||||
|
Пример 4
|
||||||
|
Выразить тройной интеграл
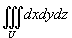 через повторные интегралы шестью различными способами. Область U расположена в первом октанте и ограничена цилиндром через повторные интегралы шестью различными способами. Область U расположена в первом октанте и ограничена цилиндром
Решение. 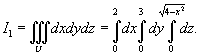  Тогда 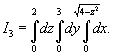 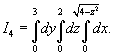 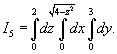 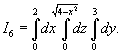 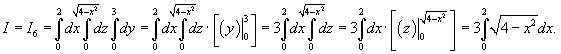 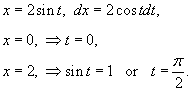 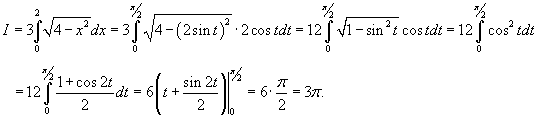 |
||||||