|
Повторные интегралы
|
||||||
|
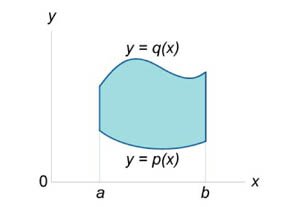
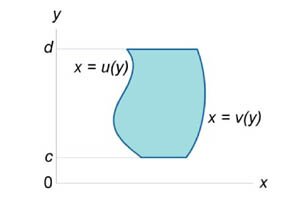
Области интегрирования I и II типа
Двойные интегралы вычисляются, как правило, с помощью повторных интегралов. Однако переход от двойных к повторным интегралам возможен не для произвольной области интегрирования R, а для областей определенного типа. Введем понятия областей интегрирования типа I и II.Определение 1. Говорят, что область R на плоскости относится к типу I или является элементарной относительно оси Oy, если она лежит между графиками двух непрерывных функций, зависящих от x 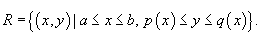 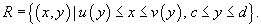
Связь между двойными и повторными интегралами
Пусть 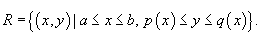 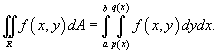 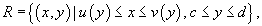 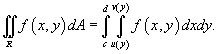 |
||||||
|
Пример 1
|
||||||
|
Найти повторный интеграл
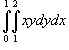 . .
Решение. 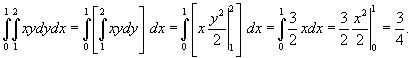 |
||||||
|
Пример 2
|
||||||
|
Найти повторный интеграл
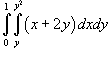 . .
Решение. 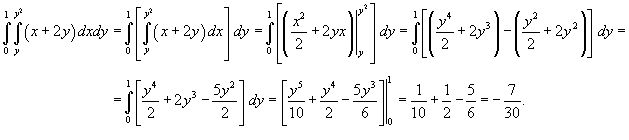 |
||||||
|
Пример 3
|
||||||
|
Вычислить
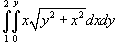 . .
Решение. 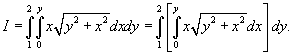 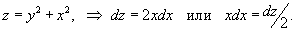 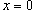 , то , то 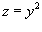 , и, соответственно, если , и, соответственно, если 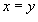 , то , то 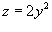 . Тогда . Тогда
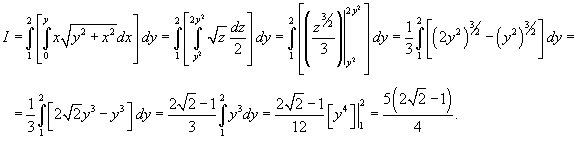 |
||||||
|
Пример 4
|
||||||
|
Вычислить
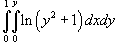 . .
Решение. 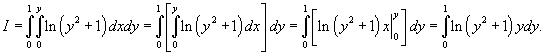 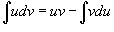 . Пусть . Пусть 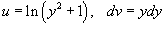 . Тогда . Тогда
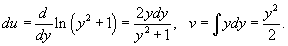 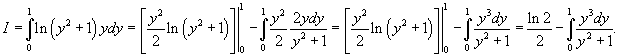 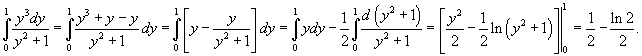 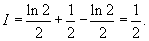 |
||||||
|
Пример 5
|
||||||
|
Изменить порядок интегрирования в повторном интеграле
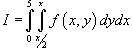 . .
Решение.  или или 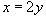 и и 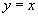 или или 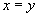 . Переменная x изменяется в интервале . Переменная x изменяется в интервале 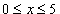 . Изменяя порядок интегрирования, исходный интеграл можно записать в виде суммы следующих двух повторных интегралов: . Изменяя порядок интегрирования, исходный интеграл можно записать в виде суммы следующих двух повторных интегралов:

|
||||||