|
Тригонометрические и гиперболические подстановки
|
|
В данной секции мы рассмотрим вычисление интегралов вида
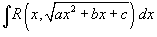 , где R - рациональная функция x и квадратного корня , где R - рациональная функция x и квадратного корня 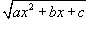 . .Предварительно преобразуем квадратичную функцию под знаком корня, выделив в ней полный квадрат: 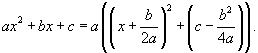 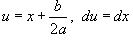 , мы получим один из следующих 3 интегралов в зависимости от значений коэффициентов , мы получим один из следующих 3 интегралов в зависимости от значений коэффициентов 1. Интегралы вида Тригонометрическая подстановка:
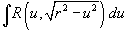 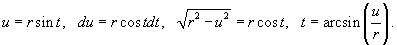 2. Интегралы вида Тригонометрическая подстановка:
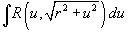 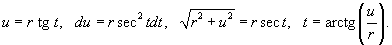 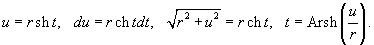 3. Интегралы вида Тригонометрическая подстановка:
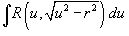 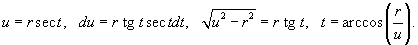 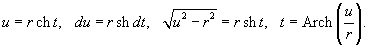
|
|
Пример 1
|
|
Вычислить интеграл
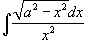 . .
Решение. 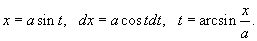 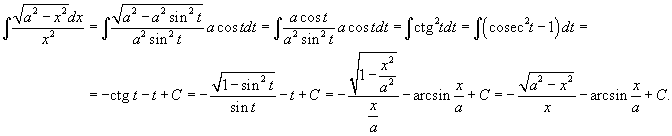 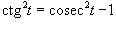 . . |
|
Пример 2
|
|
Вычислить интеграл
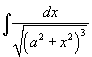 . .
Решение. 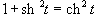 , интеграл равен , интеграл равен
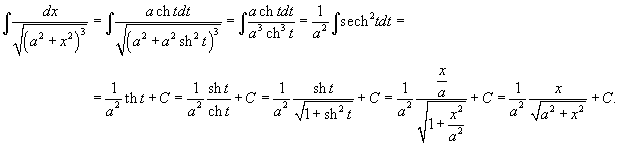 |
|
Пример 3
|
|
Вычислить интеграл
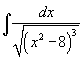 . .
Решение. 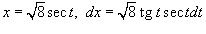 . Применив соотношение . Применив соотношение 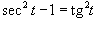 , получаем , получаем
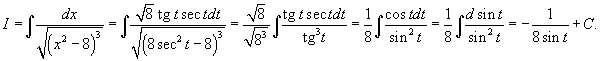 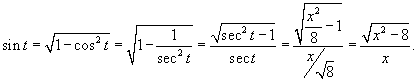 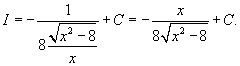 |
|
Пример 4
|
|
Вычислить интеграл
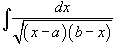 . .
Решение. 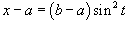 . Следовательно, . Следовательно,
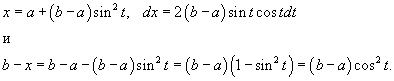 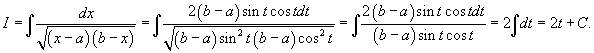 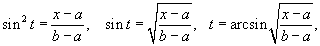 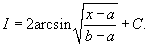 |
|
Пример 5
|
|
Вычислить интеграл
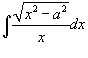 . .
Решение. 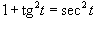 . .
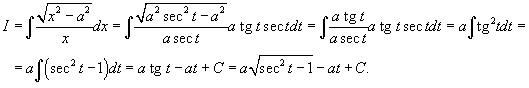 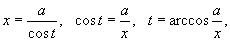 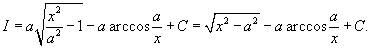 |
|
Пример 6
|
|
Найти интеграл
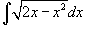 . .
Решение. 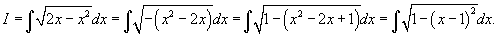 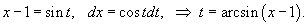 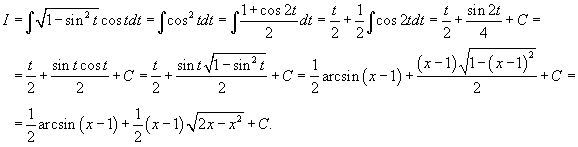 |
|
Пример 7
|
|
Найти интеграл
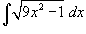 . .
Решение. 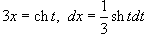 . Так как . Так как 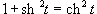 , то интеграл записывается в виде , то интеграл записывается в виде
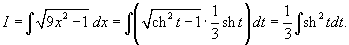 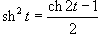 . Тогда . Тогда
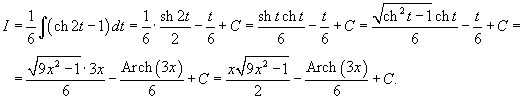 |
|
Пример 8
|
|
Вычислить интеграл
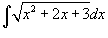 . .
Решение. 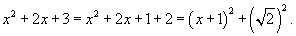 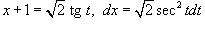 и соотношение и соотношение 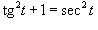 , находим интеграл , находим интеграл
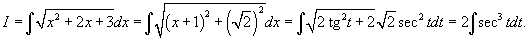 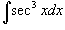 вычислен в примере 9 на странице Интегрирование некоторых классов тригонометрических функций . Окончательный ответ равен вычислен в примере 9 на странице Интегрирование некоторых классов тригонометрических функций . Окончательный ответ равен
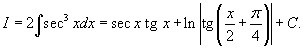 |
|
Пример 9
|
|
Найти интеграл
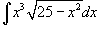 . .
Решение.  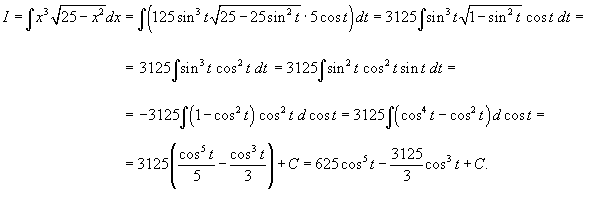 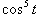 и и 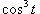 через x: через x:
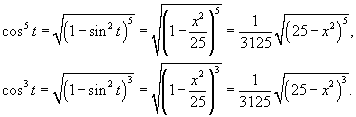 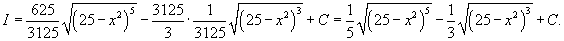 |
|
Пример 10
|
|
Вычислить интеграл
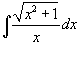 . .
Решение. 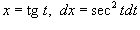 , получаем , получаем
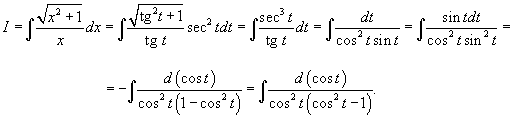 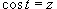 . Интеграл примет вид . Интеграл примет вид
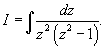 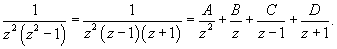 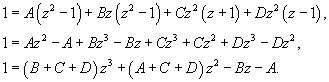 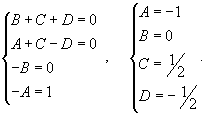 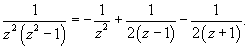 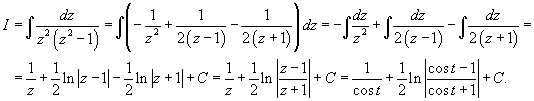 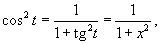 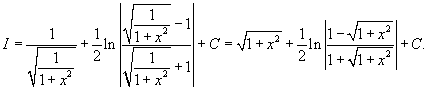 |
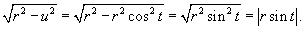
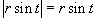 .
.