|
Интегрирование некоторых классов тригонометрических функций
|
|
В данном разделе мы рассмотрим 8 специальных классов интегралов от тригонометрических функций. Для каждого класса применяются определенные преобразования и подстановки, позволяющие получить аналитическое решение.
1. Интегралы вида Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность:
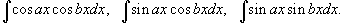 2. Интегралы вида Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования:
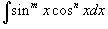
3. Интегралы вида Степень подынтегрального выражения в данном интеграле можно понизить с помошью тригонометрического соотношения 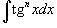 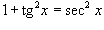 и формулы редукции и формулы редукции
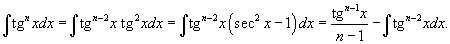 4. Интегралы вида Здесь степень подынтегрального выражения понижается с помошью соотношения 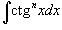 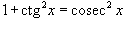 и формулы редукции и формулы редукции
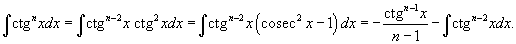 5. Интегралы вида Данный тип интеграла упрощается с помощью следующей формулы редукции:
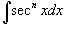 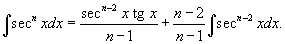 6. Интегралы вида Аналогично предыдущим пунктам, интеграл упрощается с помощью формулы
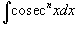 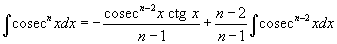 7. Интегралы вида
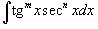
8. Интегралы вида
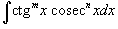
|
|
Пример 1
|
|
Вычислить интеграл
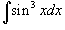 . .
Решение. 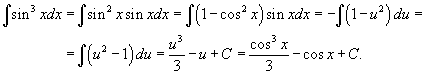 |
|
Пример 2
|
|
Вычислить
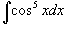 . .
Решение. 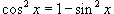 , получаем , получаем
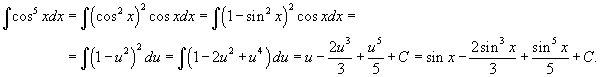 |
|
Пример 3
|
|
Вычислить интеграл
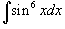 . .
Решение. 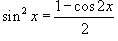 и и 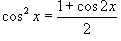 , можно записать , можно записать
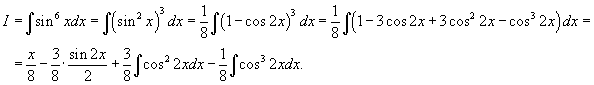 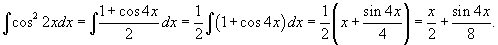 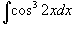 , сделаем замену , сделаем замену 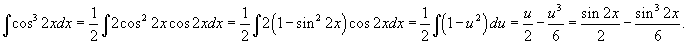 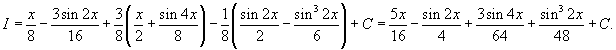 |
|
Пример 4
|
|
Найти интеграл
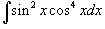 . .
Решение. 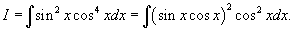 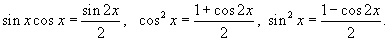 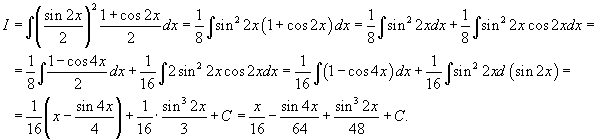 |
|
Пример 5
|
|
Найти интеграл
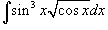 . .
Решение. 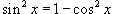 , получаем , получаем
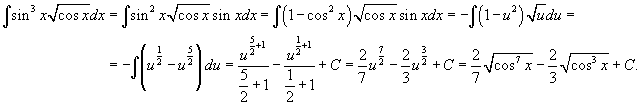 |
|
Пример 6
|
|
Вычислить интеграл
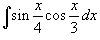 . .
Решение. 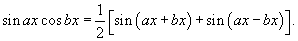 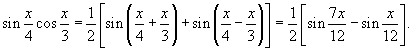 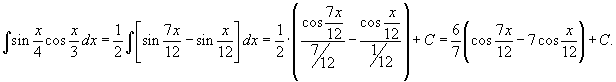 |
|
Пример 7
|
|
Вычислить интеграл
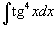 . .
Решение.  . Получаем . Получаем
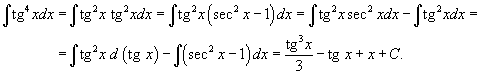 |
|
Пример 8
|
|
Вычислить интеграл
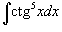 . .
Решение. 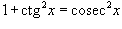 , находим , находим
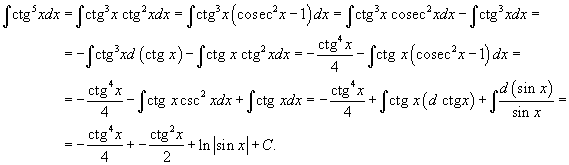 |
|
Пример 9
|
|
Вычислить
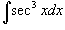 . .
Решение. 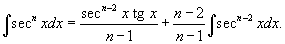 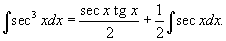 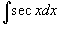 является табличным и равен является табличным и равен 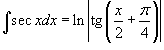 . (Он легко вычисляется с помощью универсальной тригонометрической подстановки . (Он легко вычисляется с помощью универсальной тригонометрической подстановки 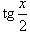 .) В результате интеграл равен .) В результате интеграл равен
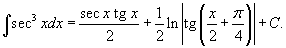 |
|
Пример 10
|
|
Вычислить интеграл
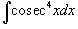 . .
Решение. 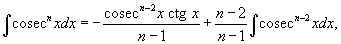 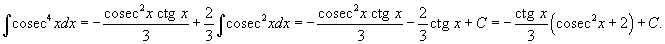 |
|
Пример 11
|
|
Найти интеграл
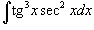 . .
Решение. 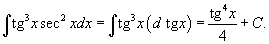 |
|
Пример 12
|
|
Найти интеграл
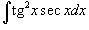 . .
Решение.  . Тогда интеграл принимает вид . Тогда интеграл принимает вид
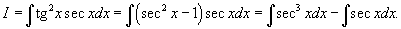 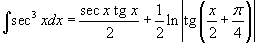 (см. пример 9), а интеграл (см. пример 9), а интеграл 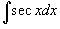 является табличным и равен является табличным и равен 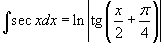 , то получаем окончательный ответ в виде , то получаем окончательный ответ в виде
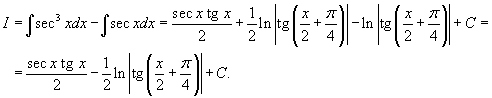 |
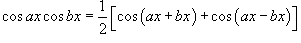
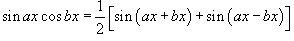
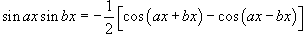
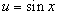 .
. .
.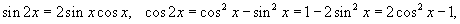
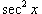 отделяется и используется для преобразования дифференциала. В результате весь интеграл (включая дифференциал) выражается через функцию
отделяется и используется для преобразования дифференциала. В результате весь интеграл (включая дифференциал) выражается через функцию 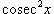 отделяется и используется для преобразования дифференциала. В результате подынтегральная функция и дифференциал выражаются через
отделяется и используется для преобразования дифференциала. В результате подынтегральная функция и дифференциал выражаются через