|
Независимость криволинейных интегралов от пути интегрирования
|
|
Определения
Криволинейный интеграл второго рода от векторной функции 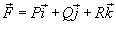 не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция 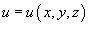 , такая, что , такая, что
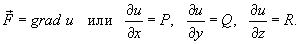 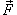 вдоль кривой C от точки A до точки B выражается формулой вдоль кривой C от точки A до точки B выражается формулой
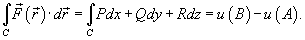 Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение 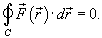 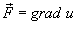 , называется потенциальным, а функция , называется потенциальным, а функция 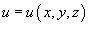 называется потенциалом. называется потенциалом.
Признак потенциальности поля
Криволинейный интеграл II рода от функции 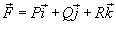 не зависит от пути интегрирования, если не зависит от пути интегрирования, если
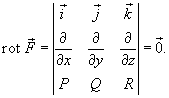 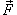 имеет непрерывные частные производные по переменным x, y и z. имеет непрерывные частные производные по переменным x, y и z.Если криволинейный интеграл рассматривается в плоскости Oxy, то в случае потенциального поля будет справедливо соотношение 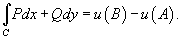 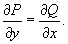 |
|
Пример 1
|
|
Вычислить криволинейный интеграл
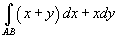 для двух путей интегрирования: для двух путей интегрирования:1) AB − отрезок прямой от точки 2) AB − участок параболы 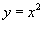 от от Решение. 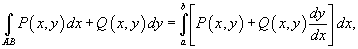 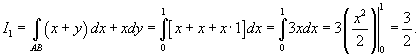 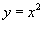 , мы имеем , мы имеем
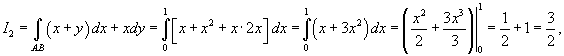 Применим признак 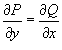 для проверки поля на потенциальность. для проверки поля на потенциальность.
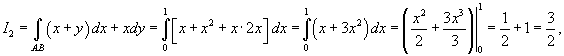 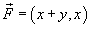 является потенциальным, что и объясняет независимость криволинейного интеграла от пути интегрирования. является потенциальным, что и объясняет независимость криволинейного интеграла от пути интегрирования. |
|
Пример 2
|
|
Показать, что криволинейный интеграл
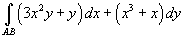 , где точки A, B имеют координаты , где точки A, B имеют координаты Решение. 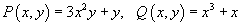 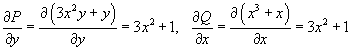 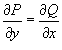 выполнено, то данное векторное поле выполнено, то данное векторное поле 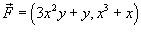 потенциально и, следовательно, криволинейный интеграл не зависит от пути интегрирования. Заметим, что потенциально и, следовательно, криволинейный интеграл не зависит от пути интегрирования. Заметим, что
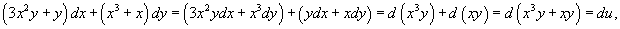 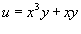 . Тогда по формуле . Тогда по формуле
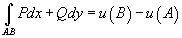 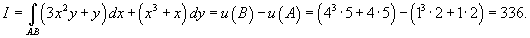 |
|
Пример 3
|
|
Определить, является ли векторное поле
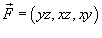 потенциальным? потенциальным?
Решение. 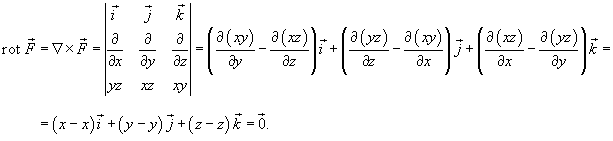 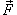 потенциально. потенциально. |
|
Пример 4
|
|
Определить, является ли векторное поле
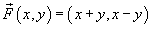 потенциальным? Если да, то найти его потенциал. потенциальным? Если да, то найти его потенциал.
Решение. 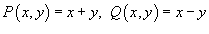 . Легко видеть, что . Легко видеть, что
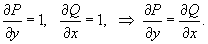 Чтобы найти потенциал, сначала проинтегрируем 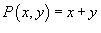 по отношению к x. по отношению к x.
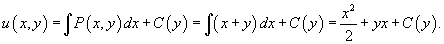 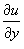 к к 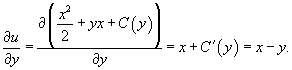 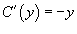 . Тогда . Тогда
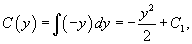 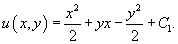 |
|
Пример 5
|
|
Определить, является ли потенциальным векторное поле
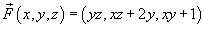 ? Если да, найти его потенциал. ? Если да, найти его потенциал.
Решение. 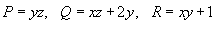 . Вычислим ротор заданного поля. . Вычислим ротор заданного поля.
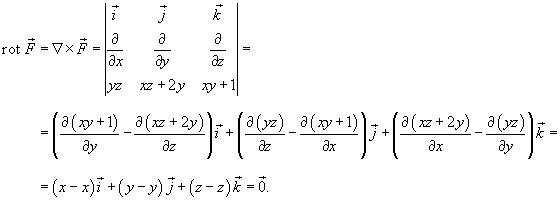 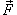 потенциально. Чтобы найти его потенциал, проинтегрируем потенциально. Чтобы найти его потенциал, проинтегрируем 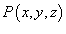 по переменной x. по переменной x.
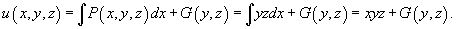 Теперь продифференцируем потенциал u по переменной y и приравняем 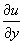 к Q. к Q.
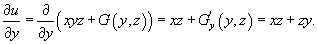 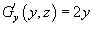 . .Для определения 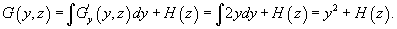 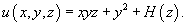 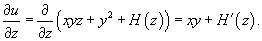 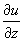 равным равным 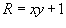 , находим , находим
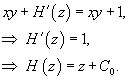 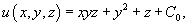 |