|
Колебания в электрических цепях
|
||||||||||||||||||
|
Дифференциальные уравнения RLC-цепей
В электрической цепи, содержащей сопротивление R, индуктивность L и емкость C, могут возбуждаться электрические колебания. С точки зрения топологии чаще всего рассматриваются два вида электрических цепей: последовательная RLC-цепь (рисунок 1) и параллельная RLC-цепь (рисунок 2).
Напряжения VR, VC, VL, соответственно, на резисторе R, конденсаторе C и катушке индуктивности L выражаются формулами 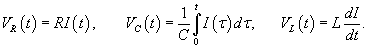 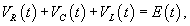 В случае постоянной э.д.с. E после подстановки выражений для VR, VC и VL и последующего дифференцирования получаем следующее дифференциальное уравнение: 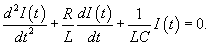 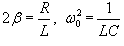 , то уравнение записывается в виде , то уравнение записывается в виде
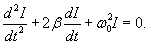 Теперь рассмотрим параллельную RLC-цепь и выведем для нее аналогичное дифференциальное уравнение. По первому закону Кирхгофа полный ток будет равен сумме токов через сопротивление R, катушку индуктивности L и конденсатор C (рисунок 2): 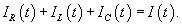 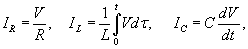 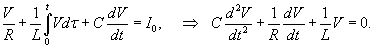
Простейший колебательный контур. Формула Томсона
В простейшем случае, когда омическое сопротивление равно нулю ( 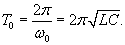
Затухающие колебания в последовательной RLC-цепи
Выше мы получили дифференциальное уравнение второго порядка, описывающее затухающие колебания в последовательном RLC-контуре, которое записывается как
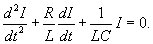 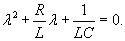 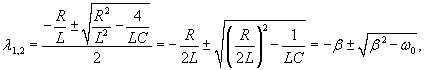 В зависимости от значений параметров R, L, C могут возникнуть три режима.
Случай 1. В этом случае оба корня характеристического уравнения λ1 и λ2 действительны, различны и отрицательны. Общее решение дифференциального уравнения определяется формулой
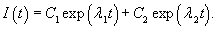
Случай 2. Данный режим можно назвать граничным или критическим. Здесь оба корня характеристического уравнения совпадают, но при этом являются действительными и отрицательными. Общее решение уравнения выражается функцией

Случай 3. В этом случае корни характеристического уравнения являются комплексно-сопряженными. В электрической цепи возникают затухающие колебания. Закон изменения тока имеет вид
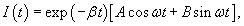 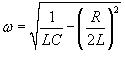 − частота колебаний, A, B − постоянные интегрирования, зависящие от начальных условий. Заметим, что частота затухающих колебаний ω меньше резонансной частоты ω0 колебательного контура. Типичный вид кривой − частота колебаний, A, B − постоянные интегрирования, зависящие от начальных условий. Заметим, что частота затухающих колебаний ω меньше резонансной частоты ω0 колебательного контура. Типичный вид кривой
Вынужденные колебания и резонанс
Если колебательный контур содержит генератор с периодически изменяющейся э.д.с., то в нем устанавливаются вынужденные колебания. Если э.д.с. E источника тока изменяется по закону
  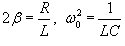 . .Данное уравнение аналогично уравнению вынужденных колебаний пружинного маятника, рассмотренного на странице Механические колебания. Его общее решение представляет собой сумму двух слагаемых − общего решения однородного уравнения и частного решения неоднородного уравнения. При этом общее решение однородного уравнения описывает затухающий переходный процесс, по истечении которого в системе устанавливаются вынужденные колебания. Эти вынужденные колебания будут происходить по закону 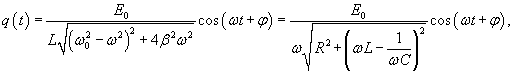 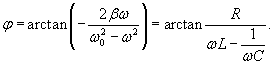 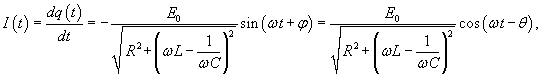 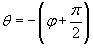 . Угол θ показывает отставание колебаний тока . Угол θ показывает отставание колебаний тока 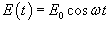 . .Амплитуда тока I0 и сдвиг фаз θ определяются формулами 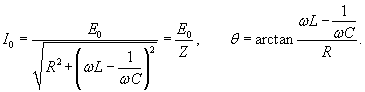 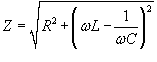 называется полным сопротивлением или импедансом контура. Она состоит из омического сопротивления R и реактивного сопротивления называется полным сопротивлением или импедансом контура. Она состоит из омического сопротивления R и реактивного сопротивления 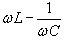 . Импеданс колебательного контура в комплексной форме записывается как . Импеданс колебательного контура в комплексной форме записывается как
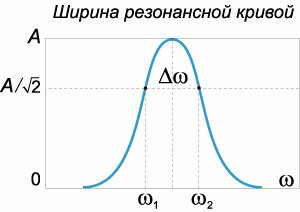
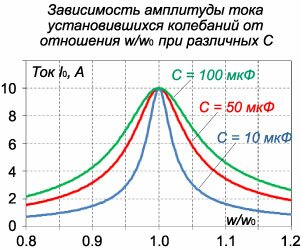
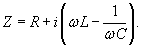 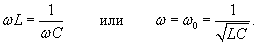 Формулу для амплитуды тока вынужденных колебаний можно преобразовать, выделив в явном виде зависимость от отношения частот 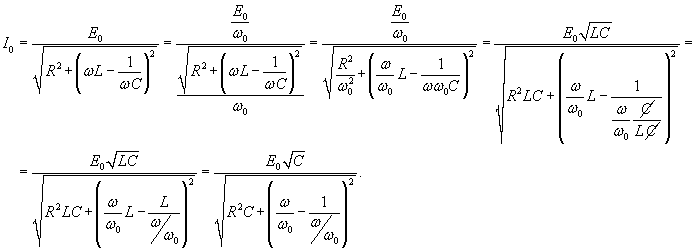
В последовательном колебательном контуре добротность вычисляется по формуле 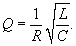 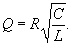 |
||||||||||||||||||
|
Пример 1
|
||||||||||||||||||
|
Электрическая цепь состоит из последовательно соединенных резистора сопротивлением
Решение. 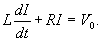 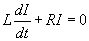 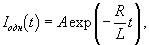 Решение неоднородного уравнения Iнеодн соответствует установившемуся режиму, при котором ток в цепи определяется лишь омическим сопротивлением R: 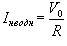 . Тогда полный ток будет изменяться по закону . Тогда полный ток будет изменяться по закону
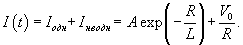 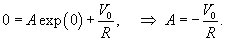 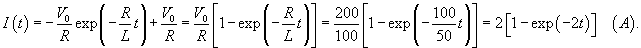 Напряжения на резисторе VR и на катушке индуктивности VL определяются следующими формулами: 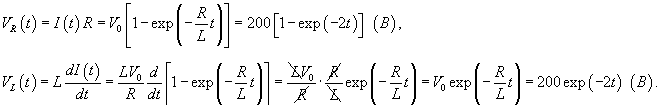
|
||||||||||||||||||
|
Пример 2
|
||||||||||||||||||
|
Электрическая цепь состоит из последовательно соединенных резистора сопротивлением
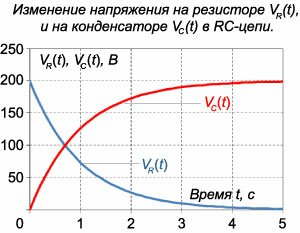
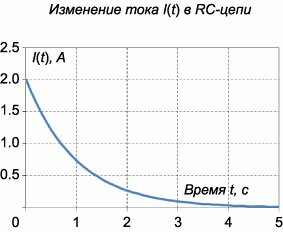
Решение. Согласно 2-му закону Кирхгофа 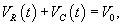 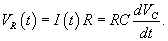 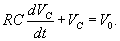 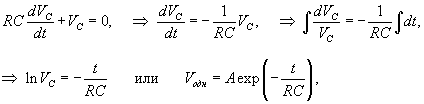 Частное решение неоднородного уравнения соответствует установившемуся режиму, при котором 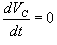 . Тогда напряжение на резисторе будет равно нулю и все напряжение будет приложено к конденсатору, то есть . Тогда напряжение на резисторе будет равно нулю и все напряжение будет приложено к конденсатору, то есть 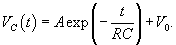 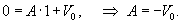 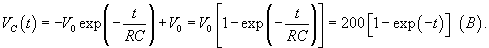 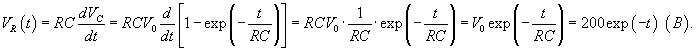 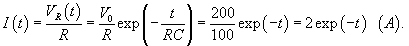
|
||||||||||||||||||
|
Пример 3
|
||||||||||||||||||
|
Электрическая цепь состоит из последовательно соединенных резистора сопротивлением
Решение. 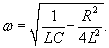 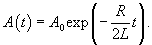 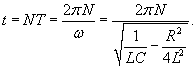 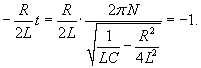 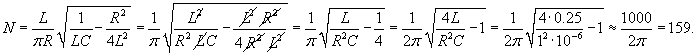 |
||||||||||||||||||
|
Пример 4
|
||||||||||||||||||
|
К последовательной цепи, состоящей из сопротивления
Решение. 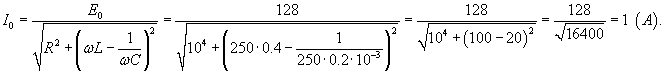 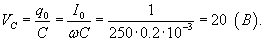 |
||||||||||||||||||