|
Механические колебания
|
||||||||||||||||||
|
Колебательные процессы встречаются повсюду в природе и технике. В астрономии планеты периодически обращаются вокруг Солнца, переменные звезды, такие как цефеиды, периодически меняют свою яркость, движение Луны вызывает приливы и отливы. В геофизике периодические процессы проявляются при изменении климата, в поведении океанических течений, в динамике циклонов и антициклонов. Внутри живых организмов происходят десятки различных периодических процессов с периодом от доли секунды до года, и т.д.
Мы начнем рассмотрение колебаний с анализа простейшей системы − гармонического осциллятора.
Свободные гармонические колебания
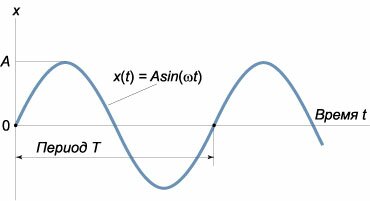
Примером такой простейшей системы является груз массы m, прикрепленный к пружине жесткостью k (рисунок 1). В идеальном случае (пренебрегая сопротивлением воздуха и внутренним трением) такая система будет совершать незатухающие гармонические колебания, при которых смещение x описывается функцией косинус или синус:
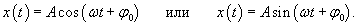 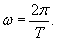
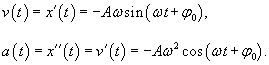 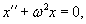 В случае груза на пружинке, возвращающая сила при малых колебаниях подчиняется закону Гука: 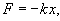 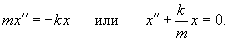 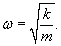 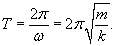 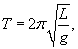 В случае физического маятника период колебаний определяется выражением 
Затухающие колебания
В реальных колебательных системах всегда присутствуют силы трения или сопротивления, которые приводят к постепенному затуханию колебаний. Во многих случаях сила сопротивления (обозначим ее Fс) пропорциональна скорости движения тела, т.е.
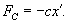 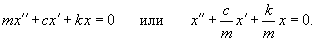 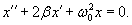 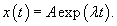 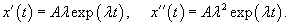 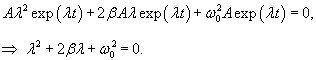 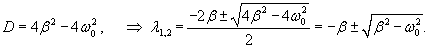
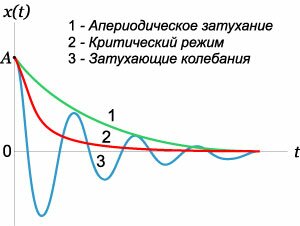
Случай 1. Режим апериодического затухания: β > ω0
В этом случае (при сильном затухании) подкоренное выражение положительно: 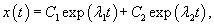
Случай 2. Граничный режим: β = ω0
В предельном случае, при 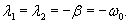 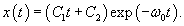 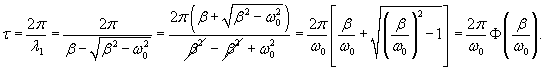 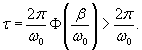
Случай 3. Режим малого затухания: β < ω0
Здесь корни характеристического уравнения являются комплексно-сопряженными:
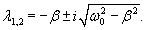 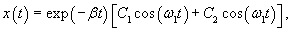 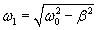 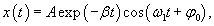
Вынужденные колебания. Резонанс
Пусть на колебательную систему действует внешняя сила, изменяющаяся со временем по гармоническому закону с частотой ω:
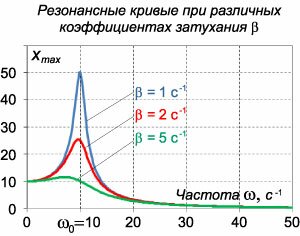
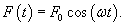 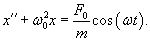 Общее решение однородного уравнения было уже получено выше. Оно записывается в виде 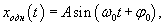 Найдем частное решение неоднородного дифференциального уравнения. Будем искать его в виде 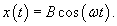 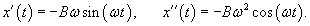 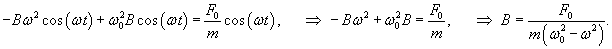 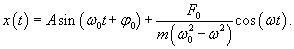 Физическая модель вынужденных колебаний получается более реалистичной, если учесть затухание колебаний. Тогда из второго закона Ньютона вытекает следующее дифференциальное уравнение: 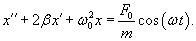 Решение однородного уравнения, как показано выше, включает в себя три возможных сценария (режим апериодического затухания, граничный режим и колебательное решение в случае малого затухания). Определим частное решение неоднородного уравнения. Здесь удобнее перейти к комплексной форме дифференциального уравнения, которое запишется как 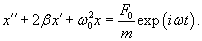 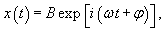 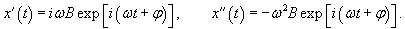  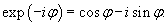 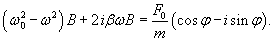 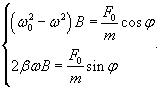 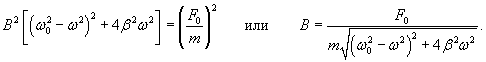  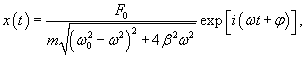 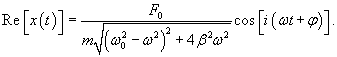 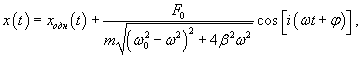 Заметим, что вследствие затухания решение однородного уравнения 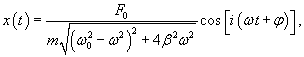 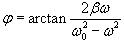 , β − коэффициент затухания. , β − коэффициент затухания.Эта формула описывает также и явление резонанса, причем максимальная амплитуда установившихся колебаний при резонансе будет конечной и равной 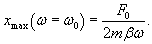 Для оценки свойств колебательной системы в окрестности резонанса используют понятие добротности. Добротность показывает во сколько раз амплитуда вынужденных колебаний при резонансе превышает их амплитуду вдали от резонанса. При стремлении частоты вынужденной силы ω к нулю амплитуда колебаний механической системы приближается к 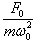 : :
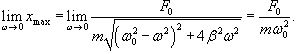 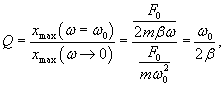 Добротность является очень полезной характеристикой. С энергетической точки зрения она показывает отношение энергии, запасенной в колебательной системе, к энергии, которую система теряет за один период колебаний. Потери энергии характеризуются также логарифмическим декрементом затухания δ. Соотношение между добротностью Q и логарифмическим декрементом затухания δ (при малых δ) выражается простой формулой: 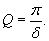
|
||||||||||||||||||
|
Пример 1
|
||||||||||||||||||
|
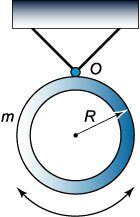
Кольцо радиуса R совершает малые колебания вокруг точки подвеса O (рисунок 6). Определить период колебаний.
Решение. 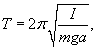 Момент инерции кольца массой m равен 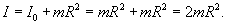 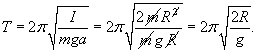 |
||||||||||||||||||
|
Пример 2
|
||||||||||||||||||
|
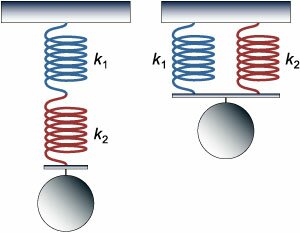
Груз подвешен на двух последовательно соединенных пружинах. Жесткость одной пружины в два раза больше жесткости другой:
Решение.
Вычислим эквивалентную жесткость в случае последовательного и параллельного соединения пружин.В случае последовательного соединения сила упругости в каждой пружине равна силе тяжести (без учета веса самих пружин). Общее удлинение равно сумме удлинений каждой пружины: 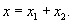 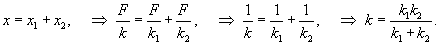 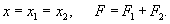 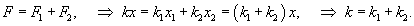 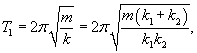 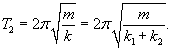 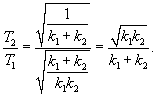 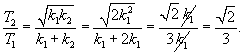 |
||||||||||||||||||
|
Пример 3
|
||||||||||||||||||
|
Найти добротность осциллятора,если через 50 колебаний амплитуда смещения уменьшилась в 2 раза.
Решение. 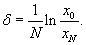 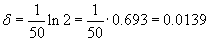 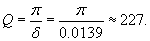 |
||||||||||||||||||