|
Ортогональные траектории
|
||||||
|
Определение и примеры
Пусть семейство кривых задано уравнением
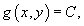 Например, ортогональной траекторией для пучка прямых линий, заданных уравнением 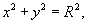
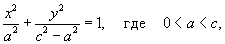 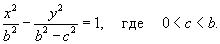
Общий метод нахождения ортогональных траекторий
Общий подход к определению ортогональных траекторий основан на решении дифференциального уравнения в частных производных:
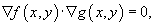 Используя определение градиента, можно записать: 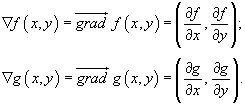 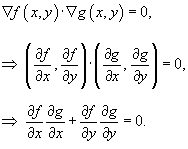
Практический алгоритм построения ортогональных траекторий
Ниже мы опишем простой алгоритм нахождения ортогональных траекторий
|
||||||
|
Пример 1
|
||||||
|
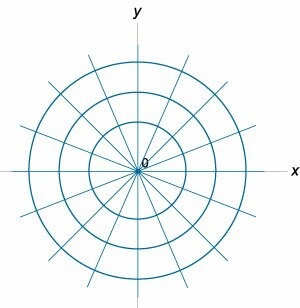
Найти ортогональные траектории семейства прямых линий
Решение. 1) Запишем дифференциальное уравнение для заданного семейства прямых 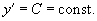  2) Заменим y' на 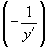 . В результате находим дифференциальное уравнение ортогональных траекторий: . В результате находим дифференциальное уравнение ортогональных траекторий:
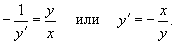 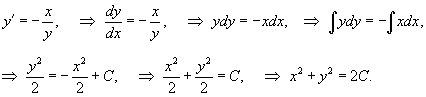 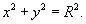 |
||||||
|
Пример 2
|
||||||
|
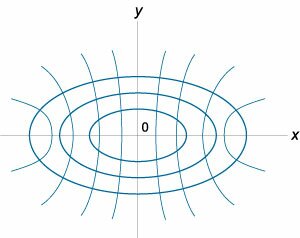
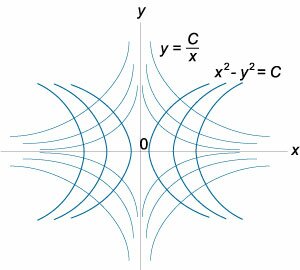
Семейство гиперболических кривых задано уравнением
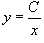 . Найти ортогональные траектории к этим кривым. . Найти ортогональные траектории к этим кривым.
Решение. 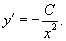 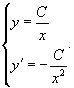 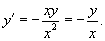 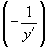 : :
 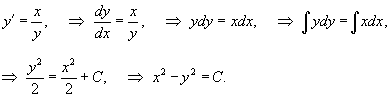
|
||||||
|
Пример 3
|
||||||
|
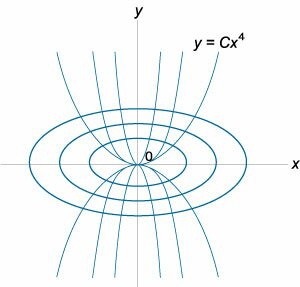
Определить ортогональные траектории для семейства кривых, заданных степенной функцией
Solution. 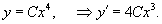 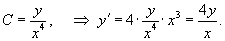 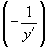 : :
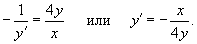 3) Интегрируя, можно найти соответствующее алгебраическое уравнение ортогональных траекторий: 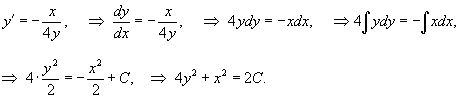 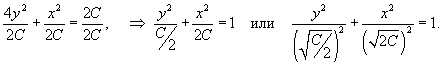 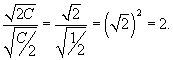 |
||||||
|
Пример 4
|
||||||
|
Определить ортогональные траектории для семейства синусоид
Решение. 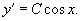 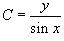 , находим дифференциальное уравнение, соответствующее синусоидальным кривым: , находим дифференциальное уравнение, соответствующее синусоидальным кривым:
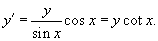 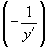 , запишем дифференциальное уравнение ортогональных кривых: , запишем дифференциальное уравнение ортогональных кривых:
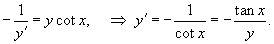 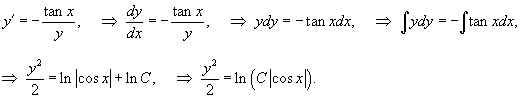 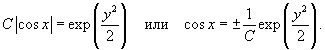 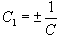 , получим окончательное неявное уравнение ортогональных кривых: , получим окончательное неявное уравнение ортогональных кривых:
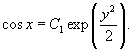 |
||||||