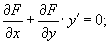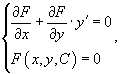|
Дифференциальные уравнения плоских кривых
|
|
Как известно, решение дифференциального уравнения изображается графически в виде семейства интегральных кривых. Можно поставить и обратную задачу: сконструировать дифференциальное уравнение для заданного семейства плоских кривых, описываемых алгебраическим уравнением!
Итак, допустим, что семейство плоских кривых описывается неявным однопараметрическим уравнением: 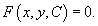
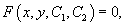 Аналогичное правило применяется и в случае n-параметрического семейства плоских кривых. |
|
Пример 1
|
|
Определить дифференциальное уравнение для семейства кривых, заданных уравнением
Решение. 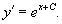 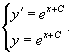 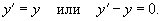 |
|
Пример 2
|
|
Вывести дифференциальное уравнение для семейства плоских кривых, заданных уравнением
Решение. 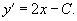 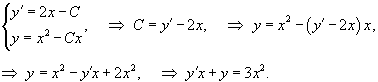 |
|
Пример 3
|
|
Составить соответствующее дифференциальное уравнение для семейства плоских кривых, заданных уравнением
Решение. 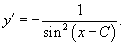 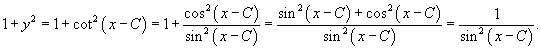 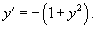 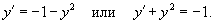 |
|
Пример 4
|
|
Семейство кривых задано функцией
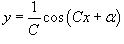 , где C − параметр, а α − некоторый произвольный угол. Записать дифференциальное уравнение для данного семейства плоских кривых. , где C − параметр, а α − некоторый произвольный угол. Записать дифференциальное уравнение для данного семейства плоских кривых.
Решение. 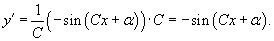 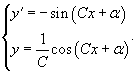 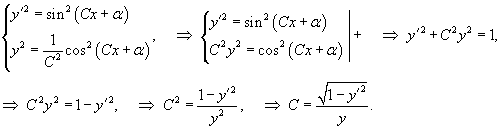 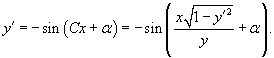 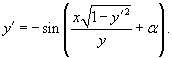 |
|
Пример 5
|
|
Вывести дифференциальное уравнение для семейства двухпараметрических плоских кривых
Решение. 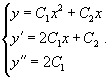 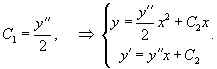 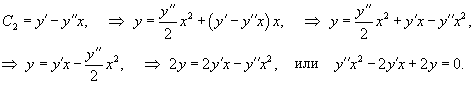 |